Công Thức Tính Hình Chữ Nhật Đầy Đủ Và Cách Ứng Dụng Bất Ngờ

Chào bạn! Chắc hẳn không ít lần trong cuộc sống, từ khi còn ngồi trên ghế nhà trường đến lúc “chạy đôn chạy đáo” lo toan việc nhà, bạn đã nghe nhắc đến hình chữ nhật rồi phải không? Đây là một trong những hình học phẳng cơ bản nhất, nhưng lại có ứng dụng rộng rãi đến không ngờ. Và để làm chủ những ứng dụng ấy, việc nắm vững Công Thức Tính Hình Chữ Nhật là điều cốt lõi. Đừng nghĩ đây chỉ là chuyện của sách vở hay những con số khô khan nhé, bởi vì hiểu rõ các công thức này sẽ giúp bạn giải quyết vô số vấn đề thực tế một cách nhanh chóng và hiệu quả. Cùng Mama Yosshino “giải mã” mọi ngóc ngách về hình chữ nhật và những công thức liên quan nhé!

Hình chữ nhật, một “gương mặt thân quen” trong thế giới hình học, không chỉ xuất hiện trong sách giáo khoa mà còn hiện diện khắp nơi quanh ta – từ viên gạch lát sàn, khung cửa sổ, màn hình điện thoại bạn đang cầm, đến mảnh vườn xinh xắn sau nhà. Tính toán liên quan đến hình chữ nhật là kỹ năng nền tảng, giúp chúng ta định lượng không gian, dự trù vật liệu, hay đơn giản là hiểu rõ hơn về thế giới xung quanh. Việc thành thạo công thức tính hình chữ nhật, bao gồm công thức tính chu vi và diện tích, chính là chìa khóa để bạn mở ra cánh cửa của sự tiện lợi và chính xác trong nhiều tình huống.

Hình Chữ Nhật Là Gì? Khái Niệm Cơ Bản Cần Nắm Vững

Vậy, cụ thể thì hình chữ nhật được định nghĩa như thế nào trong hình học? Một cách đơn giản nhất, hình chữ nhật là một tứ giác lồi có bốn góc vuông. Đúng vậy, chỉ cần bốn góc đều bằng 90 độ là đủ để nó được gọi là hình chữ nhật rồi. Từ định nghĩa này, chúng ta có thể suy ra một số tính chất rất đặc trưng và quan trọng của nó.

Bạn có thể hình dung hình chữ nhật như một cái bàn học quen thuộc. Nó có hai cặp cạnh đối diện song song và bằng nhau. Cặp cạnh dài hơn thường được gọi là chiều dài (kí hiệu là d hoặc a), và cặp cạnh ngắn hơn là chiều rộng (kí hiệu là r hoặc b). Hai đường chéo của hình chữ nhật thì bằng nhau và cắt nhau tại trung điểm của mỗi đường. Chính những tính chất này làm cho hình chữ nhật trở nên đặc biệt và dễ dàng tính toán.

Hiểu rõ khái niệm và tính chất của hình chữ nhật là bước đầu tiên và cũng là bước cực kỳ quan trọng trước khi chúng ta “lăn xả” vào các công thức tính toán. Nó giúp bạn hình dung đúng về đối tượng mình đang làm việc, tránh nhầm lẫn với các hình khác như hình vuông (một trường hợp đặc biệt của hình chữ nhật) hay hình bình hành (chỉ có các cạnh đối song song và bằng nhau, góc có thể không vuông).

Tại sao phải mất công tìm hiểu kỹ lưỡng về một hình học đơn giản như vậy? Bởi vì kiến thức nền tảng vững chắc sẽ giúp bạn không chỉ áp dụng công thức một cách máy móc, mà còn hiểu được bản chất, từ đó dễ dàng giải quyết các bài toán phức tạp hơn hay ứng dụng vào những tình huống “khó nhằn” trong thực tế.

Tại Sao Cần Nắm Vững Công Thức Tính Hình Chữ Nhật? Lợi Ích Thực Tế Bất Ngờ

Bạn có bao giờ tự hỏi tại sao các công thức toán học lại được dạy trong nhà trường không? Đơn giản là vì chúng là những công cụ mạnh mẽ giúp chúng ta giải quyết các vấn đề trong cuộc sống. Nắm vững công thức tính hình chữ nhật mang lại vô số lợi ích thiết thực mà có thể bạn chưa nghĩ tới hết.

Lợi ích đầu tiên và rõ ràng nhất là trong các bài tập toán học. Từ cấp tiểu học, bạn đã làm quen với việc tính chu vi và diện tích hình chữ nhật. Lên các cấp cao hơn, những công thức này trở thành nền tảng cho việc học về thể tích (hình hộp chữ nhật), diện tích bề mặt, và nhiều khái niệm hình học không gian khác. Việc thành thạo chúng giúp bạn tự tin hơn khi giải toán, đạt kết quả tốt hơn trong học tập.

Xa hơn nữa, những công thức này là “người bạn đồng hành” đắc lực trong rất nhiều công việc và hoạt động đời thường.

• Trong xây dựng và sửa chữa nhà cửa: Bạn cần lát gạch cho một căn phòng hình chữ nhật? Công thức diện tích sẽ giúp bạn tính toán số lượng gạch cần mua. Muốn sơn tường? Diện tích các bức tường hình chữ nhật cho bạn biết lượng sơn. Lắp phào chỉ quanh trần nhà? Chu vi căn phòng là thứ bạn cần tính.
• Trong làm vườn: Bạn muốn rào quanh mảnh vườn hình chữ nhật để trồng rau? Công thức chu vi cho biết độ dài hàng rào cần thiết. Muốn bón phân cho toàn bộ luống rau? Diện tích luống sẽ giúp bạn ước tính lượng phân bón hợp lý.
• Trong thiết kế và trang trí nội thất: Sắp xếp đồ đạc trong phòng, trải thảm, treo tranh ảnh… đều liên quan đến việc ước lượng không gian hình chữ nhật và tính toán diện tích, chu vi để mọi thứ “ăn khớp” với nhau.
• Trong các ngành nghề khác: Kiến trúc sư, kỹ sư, thợ mộc, thậm chí là người bán hàng (tính diện tích vải, thảm) hay nông dân (tính diện tích đất canh tác) đều sử dụng các công thức này một cách thường xuyên.

Ngoài ra, việc tính toán còn giúp bạn phát triển tư duy logic, khả năng ước lượng, và kỹ năng giải quyết vấn đề một cách có hệ thống. Mỗi khi áp dụng công thức, bạn đang thực hành việc phân tích thông tin, lựa chọn phương pháp phù hợp và kiểm tra kết quả. Đó là những kỹ năng vô giá không chỉ trong toán học mà còn trong mọi lĩnh vực của cuộc sống.

Thấy chưa? Những công thức đơn giản ấy lại có sức mạnh to lớn đến vậy. Nắm chắc chúng trong tay, bạn sẽ thấy nhiều công việc trở nên dễ dàng và hiệu quả hơn rất nhiều.

Hai Công Thức “Vàng” Để Tính Toán Hình Chữ Nhật: Chu Vi Và Diện Tích

Khi nói đến công thức tính hình chữ nhật, người ta thường nhắc đến hai đại lượng cơ bản và quan trọng nhất: chu vi và diện tích. Mỗi công thức phục vụ cho một mục đích tính toán khác nhau, và cả hai đều dựa trên hai kích thước chính của hình chữ nhật là chiều dài và chiều rộng.

Hãy cùng “mổ xẻ” từng công thức một để hiểu rõ hơn nhé.

Công Thức Tính Chu Vi Hình Chữ Nhật Chi Tiết

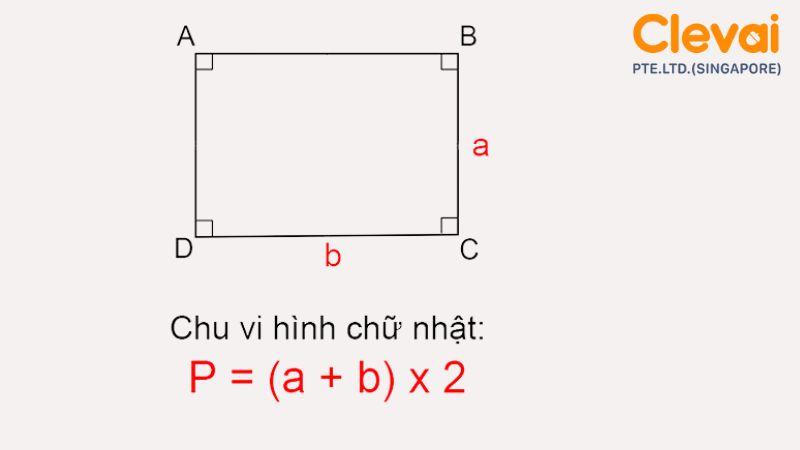
Chu vi của một hình phẳng là tổng độ dài của tất cả các cạnh bao quanh hình đó. Tưởng tượng bạn đang đi bộ dọc theo viền của một sân bóng đá hình chữ nhật; quãng đường bạn đi chính là chu vi của sân.

Đối với hình chữ nhật, có hai cạnh dài (chiều dài) và hai cạnh ngắn (chiều rộng). Vì các cạnh đối diện bằng nhau, để tính chu vi, chúng ta chỉ cần cộng độ dài của cả bốn cạnh lại.

Nếu gọi chiều dài là d và chiều rộng là r, thì chu vi P của hình chữ nhật sẽ là:
P = d + r + d + r

Gom các số hạng giống nhau lại, ta có:
P = 2 * d + 2 * r

Hay gọn gàng hơn, ta dùng phép nhân trước phép cộng (nhân một tổng với một số):
P = (d + r) * 2

Đây chính là công thức tính chu vi hình chữ nhật “kinh điển” mà chúng ta học từ những lớp đầu cấp 1. Nó nói rằng, để tính chu vi hình chữ nhật, ta lấy tổng của chiều dài và chiều rộng rồi nhân với 2.

Đơn vị của chu vi là đơn vị độ dài, ví dụ như centimet (cm), mét (m), kilômét (km)… Nếu chiều dài và chiều rộng cùng đơn vị, chu vi sẽ có đơn vị đó. Ví dụ, nếu chiều dài và chiều rộng đều tính bằng mét, thì chu vi sẽ tính bằng mét.

Hiểu tại sao công thức này lại là (d + r) * 2 rất đơn giản. Chiều dài cộng với chiều rộng chính là tổng độ dài của một cặp cạnh kề nhau. Vì hình chữ nhật có hai cặp cạnh kề nhau như vậy (và tổng độ dài của mỗi cặp đều bằng nhau), nên ta nhân tổng d + r với 2. Thật logic phải không nào?

Công Thức Tính Diện Tích Hình Chữ Nhật Cực Đơn Giản

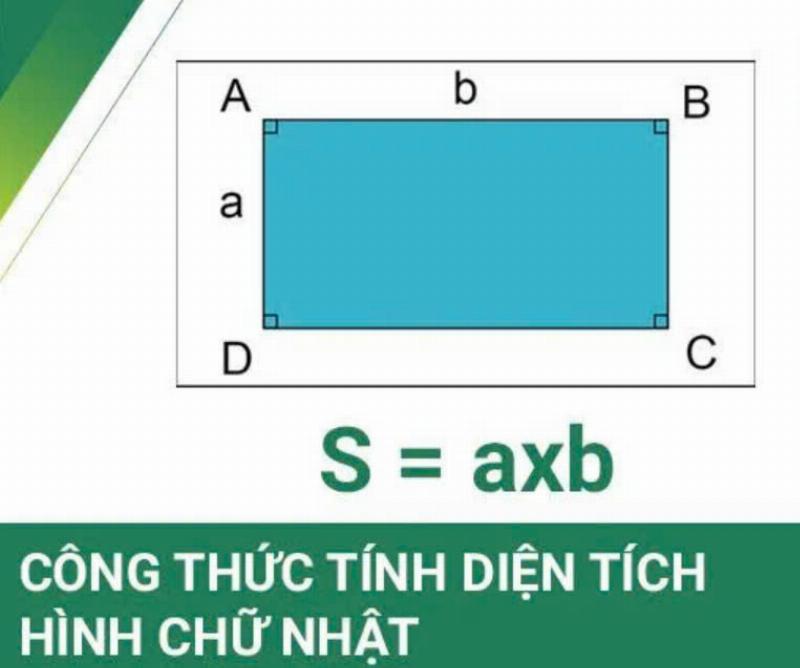
Diện tích của một hình phẳng là phần không gian bề mặt mà hình đó chiếm chỗ. Tưởng tượng bạn đang lát gạch cho sàn nhà hình chữ nhật; diện tích sàn nhà cho bạn biết tổng “không gian” mà các viên gạch sẽ phủ đầy.

Để tính diện tích, chúng ta xem hình chữ nhật như được tạo thành từ việc xếp các ô vuông đơn vị (mỗi ô vuông có cạnh bằng 1 đơn vị đo) “lấp đầy” bề mặt của nó.

Nếu chiều dài là d đơn vị và chiều rộng là r đơn vị, bạn có thể hình dung việc xếp d ô vuông theo chiều dài và r ô vuông theo chiều rộng. Tổng số ô vuông nhỏ lấp đầy hình chữ nhật sẽ là tích của số ô vuông theo mỗi chiều.

Vì vậy, diện tích A của hình chữ nhật được tính bằng công thức:
A = d * r

Đây là công thức tính diện tích hình chữ nhật đơn giản đến không ngờ! Chỉ cần lấy chiều dài nhân với chiều rộng là xong.

Đơn vị của diện tích là đơn vị diện tích, được tạo ra bằng cách bình phương đơn vị độ dài. Ví dụ, nếu chiều dài và chiều rộng tính bằng mét, thì diện tích tính bằng mét vuông (m²). Nếu tính bằng centimet, diện tích là centimet vuông (cm²). Các đơn vị diện tích phổ biến khác bao gồm kilômét vuông (km²), héc-ta (ha – thường dùng cho đất đai, 1 ha = 10.000 m²), mẫu Anh (acre – đơn vị của Anh/Mỹ).

Công thức A = d * r phản ánh bản chất của diện tích như là “lượng không gian 2 chiều” mà hình chiếm giữ. Nó là cơ sở cho việc tính diện tích của nhiều hình phức tạp hơn (bằng cách chia nhỏ chúng thành các hình chữ nhật) và là nền tảng cho khái niệm thể tích.

Nắm chắc hai công thức P = (d + r) * 2 và A = d * r là bạn đã có trong tay bộ công cụ cơ bản nhất để giải quyết mọi vấn đề liên quan đến hình chữ nhật. Giờ thì cùng xem cách áp dụng chúng vào thực tế nhé!

Làm Thế Nào Để Áp Dụng Công Thức Tính Chu Vi Hình Chữ Nhật? Ví Dụ Minh Họa Chi Tiết

Việc áp dụng công thức tính hình chữ nhật cho chu vi không hề khó khăn chút nào. Chỉ cần bạn biết được chiều dài và chiều rộng của hình chữ nhật đó, bạn hoàn toàn có thể tính toán được chu vi của nó. Dưới đây là các bước thực hiện và một vài ví dụ cụ thể để bạn dễ hình dung.

Các bước tính chu vi hình chữ nhật:

1. Xác định chiều dài (d) và chiều rộng (r) của hình chữ nhật. Đảm bảo cả hai đều sử dụng cùng một đơn vị đo (ví dụ: cùng là mét, cùng là centimet). Nếu đơn vị khác nhau, bạn cần thực hiện chuyển đổi đơn vị trước khi tính.
2. Áp dụng công thức: P = (d + r) * 2.
3. Thực hiện phép tính để tìm ra giá trị của chu vi P.
4. Ghi đơn vị đo tương ứng vào kết quả cuối cùng.

Ví dụ 1: Một mảnh vườn hình chữ nhật có chiều dài 15 mét và chiều rộng 10 mét. Tính chu vi mảnh vườn đó.

• Bước 1: Chiều dài d = 15 m, Chiều rộng r = 10 m. Đơn vị đã giống nhau (mét).
• Bước 2: Áp dụng công thức P = (d + r) * 2.
• Bước 3: P = (15 + 10) * 2 = 25 * 2 = 50.
• Bước 4: Kết quả là 50 mét.

Vậy, chu vi mảnh vườn đó là 50 mét. Nếu bạn muốn rào quanh vườn, bạn sẽ cần 50 mét hàng rào (tạm bỏ qua phần cổng ra vào).

Ví dụ 2: Một chiếc bàn học có mặt bàn hình chữ nhật với chiều dài 120 cm và chiều rộng 60 cm. Tính chu vi mặt bàn.

• Bước 1: Chiều dài d = 120 cm, Chiều rộng r = 60 cm. Đơn vị đã giống nhau (centimet).
• Bước 2: Áp dụng công thức P = (d + r) * 2.
• Bước 3: P = (120 + 60) * 2 = 180 * 2 = 360.
• Bước 4: Kết quả là 360 cm.

Chu vi mặt bàn là 360 cm, hay 3.6 mét. Nếu bạn muốn viền xung quanh mặt bàn bằng một loại nẹp, bạn cần mua nẹp dài 3.6 mét.

Ví dụ 3 (Có đổi đơn vị): Một căn phòng hình chữ nhật có chiều dài 5 mét và chiều rộng 350 cm. Tính chu vi căn phòng.

• Bước 1: Chiều dài d = 5 mét. Chiều rộng r = 350 cm. Đơn vị chưa giống nhau. Ta cần đổi 350 cm sang mét. 1 mét = 100 cm, vậy 350 cm = 350 / 100 = 3.5 mét.
  Lúc này: Chiều dài d = 5 m, Chiều rộng r = 3.5 m.
• Bước 2: Áp dụng công thức P = (d + r) * 2.
• Bước 3: P = (5 + 3.5) * 2 = 8.5 * 2 = 17.
• Bước 4: Kết quả là 17 mét.

Chu vi căn phòng là 17 mét. Việc chuyển đổi đơn vị là cực kỳ quan trọng để đảm bảo kết quả tính toán chính xác.

Để hiểu sâu hơn và thực hành nhiều dạng bài tập về cách tính chu vi hình chữ nhật, bạn có thể tìm đọc thêm các tài liệu chuyên sâu. Việc luyện tập với nhiều con số khác nhau và các tình huống thực tế sẽ giúp bạn thành thạo kỹ năng này.

Làm Thế Nào Để Áp Dụng Công Thức Tính Diện Tích Hình Chữ Nhật? Hướng Dẫn Từng Bước

Sau khi đã nắm vững cách tính chu vi, việc tính diện tích hình chữ nhật còn đơn giản hơn nhiều. Chỉ cần một phép nhân là bạn đã có ngay kết quả.

Các bước tính diện tích hình chữ nhật:

1. Xác định chiều dài (d) và chiều rộng (r) của hình chữ nhật. Tương tự như tính chu vi, cả hai kích thước này phải dùng chung một đơn vị đo. Nếu khác đơn vị, hãy chuyển đổi trước.
2. Áp dụng công thức: A = d * r.
3. Thực hiện phép tính để tìm ra giá trị của diện tích A.
4. Ghi đơn vị đo diện tích (đơn vị độ dài bình phương) vào kết quả cuối cùng.

Ví dụ 1: Một mảnh giấy hình chữ nhật có chiều dài 20 cm và chiều rộng 15 cm. Tính diện tích mảnh giấy đó.

• Bước 1: Chiều dài d = 20 cm, Chiều rộng r = 15 cm. Đơn vị đã giống nhau (centimet).
• Bước 2: Áp dụng công thức A = d * r.
• Bước 3: A = 20 * 15 = 300.
• Bước 4: Kết quả là 300 cm².

Vậy, diện tích mảnh giấy đó là 300 cm². Điều này có nghĩa là mảnh giấy đó có thể được “lấp đầy” bởi 300 ô vuông nhỏ có cạnh dài 1 cm.

Ví dụ 2: Một sân chơi hình chữ nhật có chiều dài 30 mét và chiều rộng 20 mét. Tính diện tích sân chơi.

• Bước 1: Chiều dài d = 30 m, Chiều rộng r = 20 m. Đơn vị đã giống nhau (mét).
• Bước 2: Áp dụng công thức A = d * r.
• Bước 3: A = 30 * 20 = 600.
• Bước 4: Kết quả là 600 m².

Diện tích sân chơi là 600 mét vuông. Nếu bạn muốn trải thảm cỏ cho sân chơi này, bạn cần mua đủ thảm cỏ để phủ 600 mét vuông.

Ví dụ 3 (Có đổi đơn vị và ứng dụng thực tế): Một căn phòng hình chữ nhật có chiều dài 6 mét và chiều rộng 400 cm. Bạn muốn lát sàn gỗ cho căn phòng này. Giá sàn gỗ là 250.000 VNĐ/m². Hỏi bạn cần bao nhiêu tiền để mua đủ sàn gỗ?

• Bước 1: Chiều dài d = 6 mét. Chiều rộng r = 400 cm. Đơn vị chưa giống nhau. Đổi 400 cm = 400 / 100 = 4 mét.
  Lúc này: Chiều dài d = 6 m, Chiều rộng r = 4 m.
• Bước 2: Áp dụng công thức tính diện tích: A = d * r.
• Bước 3: A = 6 * 4 = 24.
• Bước 4: Kết quả diện tích là 24 m².
• Bước 5 (Ứng dụng): Tính tổng số tiền cần mua sàn gỗ. Vì 1 m² sàn gỗ giá 250.000 VNĐ, nên 24 m² sẽ có giá: 24 * 250.000 = 6.000.000 VNĐ.

Vậy, bạn cần 6.000.000 VNĐ để mua đủ sàn gỗ cho căn phòng đó (chưa tính hao hụt vật liệu).

Hình ảnh minh họa cách tính diện tích sàn nhà hình chữ nhật để lát gạch hoặc sàn gỗ trong xây dựng

Những ví dụ trên cho thấy việc áp dụng công thức tính hình chữ nhật cho diện tích đơn giản như thế nào, và nó hữu ích ra sao trong các công việc tính toán vật liệu thực tế. Chỉ cần cẩn thận với đơn vị đo, bạn sẽ có ngay kết quả chính xác.

Mở Rộng: Các Dạng Bài Tập Phổ Biến Liên Quan Đến Công Thức Tính Hình Chữ Nhật

Không phải lúc nào chúng ta cũng chỉ được cho sẵn chiều dài và chiều rộng để tính chu vi hay diện tích. Đôi khi, bài toán lại yêu cầu chúng ta đi “ngược” lại: biết diện tích hoặc chu vi và một trong hai kích thước, hãy tìm kích thước còn lại. Đây là dạng bài tập rất phổ biến trong toán học, đặc biệt là ở cấp tiểu học và trung học cơ sở. Nắm vững cách giải quyết các bài toán này sẽ củng cố thêm sự hiểu biết của bạn về công thức tính hình chữ nhật.

Làm Thế Nào Để Tìm Chiều Dài Hoặc Chiều Rộng Khi Biết Diện Tích Và Một Chiều?

Nhớ lại công thức tính diện tích: A = d * r. Đây là một phép nhân. Trong phép nhân, nếu bạn biết tích (diện tích A) và một thừa số (chiều dài d hoặc chiều rộng r), bạn có thể tìm thừa số còn lại bằng phép chia.

• Để tìm chiều dài (d) khi biết diện tích (A) và chiều rộng (r):
  d = A / r

• Để tìm chiều rộng (r) khi biết diện tích (A) và chiều dài (d):
  r = A / d

Ví dụ: Một hình chữ nhật có diện tích 120 cm². Nếu chiều rộng là 8 cm, tính chiều dài của hình chữ nhật đó.

• Ta biết A = 120 cm², r = 8 cm.
• Áp dụng công thức tìm chiều dài: d = A / r.
• d = 120 / 8 = 15.
• Vậy, chiều dài của hình chữ nhật là 15 cm. (Đơn vị của chiều dài sẽ cùng đơn vị với chiều rộng và là căn bậc hai của đơn vị diện tích).

Dạng bài này giúp rèn luyện kỹ năng suy luận ngược và áp dụng mối liên hệ giữa phép nhân và phép chia.

Làm Thế Nào Để Tìm Chiều Dài Hoặc Chiều Rộng Khi Biết Chu Vi Và Một Chiều?

Công thức tính chu vi là: P = (d + r) * 2. Đây là một biểu thức bao gồm phép cộng và phép nhân. Để tìm chiều dài hoặc chiều rộng, chúng ta cần “giải ngược” biểu thức này.

Bước đầu tiên là tìm tổng của chiều dài và chiều rộng (d + r). Từ công thức P = (d + r) * 2, ta thấy tổng (d + r) chính là một nửa chu vi.
d + r = P / 2

Sau khi có tổng của chiều dài và chiều rộng, nếu biết một trong hai, ta có thể tìm cái còn lại bằng phép trừ.

• Để tìm chiều dài (d) khi biết tổng (d + r) và chiều rộng (r):
  d = (d + r) - r
  Hay thay d + r bằng P/2:
  d = P / 2 - r

• Để tìm chiều rộng (r) khi biết tổng (d + r) và chiều dài (d):
  r = (d + r) - d
  Hay thay d + r bằng P/2:
  r = P / 2 - d

Đây là những công thức thường gặp khi học về công thức tính chiều dài, chiều rộng hình chữ nhật lớp 4 hoặc các lớp tương đương. Nó giúp học sinh làm quen với việc biến đổi công thức và giải các bài toán có nhiều bước hơn.

Ví dụ: Một hình chữ nhật có chu vi 44 mét. Nếu chiều dài là 14 mét, tính chiều rộng của hình chữ nhật đó.

• Ta biết P = 44 mét, d = 14 mét.
• Bước 1: Tính nửa chu vi: P / 2 = 44 / 2 = 22 mét. Đây chính là tổng của chiều dài và chiều rộng.
• Bước 2: Áp dụng công thức tìm chiều rộng: r = P / 2 - d.
• r = 22 - 14 = 8.
• Vậy, chiều rộng của hình chữ nhật là 8 mét.

Thử lại nhé: Chu vi = (14 + 8) 2 = 22 2 = 44 mét. Kết quả chính xác!

Hình ảnh minh họa cách tìm chiều dài hoặc chiều rộng hình chữ nhật khi biết chu vi hoặc diện tích trong bài tập toán

Bài Toán Kết Hợp Chu Vi Và Diện Tích: Ví Dụ Nâng Cao

Đôi khi, bài toán sẽ yêu cầu kết hợp cả hai công thức. Ví dụ, biết chu vi và tỉ lệ giữa chiều dài và chiều rộng, rồi yêu cầu tính diện tích. Hoặc biết diện tích và mối liên hệ giữa chiều dài/chiều rộng (ví dụ: chiều dài hơn chiều rộng bao nhiêu), rồi yêu cầu tính chu vi.

Để giải quyết các bài toán này, bạn thường cần sử dụng kiến thức về giải phương trình hoặc các dạng toán có lời văn phức tạp hơn một chút.

Ví dụ: Một hình chữ nhật có chu vi 60 cm. Chiều dài hơn chiều rộng 8 cm. Tính diện tích hình chữ nhật đó.

• Bước 1: Tính nửa chu vi: 60 / 2 = 30 cm. Đây là tổng của chiều dài và chiều rộng (d + r = 30).
• Bước 2: Ta có hai thông tin: d + r = 30 và d - r = 8. Đây là dạng toán tìm hai số khi biết tổng và hiệu.
  • Chiều dài d = (Tổng + Hiệu) / 2 = (30 + 8) / 2 = 38 / 2 = 19 cm.
  • Chiều rộng r = (Tổng - Hiệu) / 2 = (30 - 8) / 2 = 22 / 2 = 11 cm.
• Bước 3: Sau khi tìm được chiều dài và chiều rộng, áp dụng công thức tính diện tích: A = d * r.
• A = 19 * 11 = 209.
• Vậy, diện tích hình chữ nhật đó là 209 cm².

Những bài toán kết hợp này đòi hỏi bạn phải hiểu rõ các mối quan hệ giữa chu vi, diện tích, chiều dài và chiều rộng, đồng thời vận dụng các kỹ năng giải toán khác.

Những Lưu Ý Quan Trọng Khi Sử Dụng Công Thức Tính Hình Chữ Nhật

Để việc áp dụng công thức tính hình chữ nhật luôn chính xác và hiệu quả, có một vài điểm quan trọng bạn cần ghi nhớ. Đôi khi, những sai lầm nhỏ trong quá trình tính toán hoặc đo đạc có thể dẫn đến kết quả hoàn toàn sai lệch, gây ảnh hưởng không nhỏ trong thực tế.

• Nhất Quán Về Đơn Vị Đo: Đây là điều tối quan trọng! Trước khi thực hiện bất kỳ phép tính nào, hãy kiểm tra xem chiều dài và chiều rộng có đang sử dụng cùng một đơn vị đo hay không. Nếu không, bạn phải chuyển đổi một trong hai kích thước về cùng đơn vị với kích thước còn lại. Ví dụ: không thể nhân 5 mét với 50 centimet để tính diện tích; bạn cần đổi 5 mét thành 500 cm hoặc 50 cm thành 0.5 mét. Đơn vị của kết quả (chu vi hoặc diện tích) sẽ phụ thuộc vào đơn vị bạn sử dụng cho chiều dài và chiều rộng. Đơn vị chu vi là đơn vị độ dài, đơn vị diện tích là đơn vị độ dài bình phương.
• Hình Vuông Là Trường Hợp Đặc Biệt Của Hình Chữ Nhật: Đừng bao giờ quên rằng hình vuông chính là một hình chữ nhật có chiều dài bằng chiều rộng. Do đó, mọi công thức áp dụng cho hình chữ nhật đều đúng với hình vuông. Chu vi hình vuông cạnh a là P = (a + a) * 2 = 2a * 2 = 4a. Diện tích hình vuông cạnh a là A = a * a = a². Hiểu được mối liên hệ này giúp bạn tiết kiệm thời gian và không cần học thêm công thức riêng cho hình vuông nếu đã nắm vững công thức hình chữ nhật.
• Đo Đạc Thực Tế Cần Độ Chính Xác Cao: Khi áp dụng công thức vào thực tế (ví dụ: đo phòng để mua sàn gỗ), kết quả tính toán của bạn phụ thuộc hoàn toàn vào độ chính xác của việc đo đạc chiều dài và chiều rộng. Sử dụng thước đo phù hợp (thước dây dài, thước cuộn), đo cẩn thận từ mép này sang mép kia, đo ở nhiều điểm khác nhau nếu cần (ví dụ: một căn phòng không hoàn toàn thẳng hoặc vuông vắn) và lấy giá trị trung bình hoặc giá trị lớn nhất tùy vào mục đích. Sai số khi đo có thể dẫn đến việc thiếu hoặc thừa vật liệu, gây lãng phí hoặc tốn thêm chi phí.
• Kiểm Tra Lại Kết Quả: Sau khi tính toán xong, hãy dành một chút thời gian kiểm tra lại kết quả. Bạn có thể làm tròn số và ước lượng nhanh để xem kết quả có hợp lý không. Ví dụ, nếu chiều dài khoảng 10m và chiều rộng khoảng 5m, diện tích phải quanh quẩn 50m², nếu tính ra 500m² thì rõ ràng là sai. Đối với các bài toán tìm chiều dài/rộng khi biết diện tích/chu vi, hãy dùng kết quả vừa tìm được và kích thước đã cho để tính ngược lại diện tích hoặc chu vi ban đầu, xem có khớp không.
• Hiểu Rõ Ý Nghĩa Của Chu Vi Và Diện Tích: Chu vi là “đường viền” bao quanh, còn diện tích là “bề mặt” bên trong. Đừng nhầm lẫn hai khái niệm này và đơn vị của chúng. Việc phân biệt rõ ràng giúp bạn chọn đúng công thức cho từng loại bài toán.

Tuân thủ những lưu ý này sẽ giúp bạn tự tin hơn khi làm việc với công thức tính hình chữ nhật và đạt được kết quả chính xác nhất, dù là trong học tập hay trong cuộc sống hàng ngày.

Ứng Dụng Công Thức Tính Hình Chữ Nhật Trong Đời Sống Hàng Ngày: Từ Nhà Bếp Đến Sân Vườn

Bạn có tin rằng công thức tính hình chữ nhật lại hiện diện trong vô số tình huống thường ngày mà có thể bạn chưa từng để ý không? Đúng vậy, những công thức đơn giản này là công cụ đắc lực giúp chúng ta giải quyết các bài toán thực tế một cách hiệu quả. Hãy cùng điểm qua một vài ứng dụng “từ nhà bếp đến sân vườn” nhé!

• Trong Nhà Bếp:

  • Bạn muốn trải một tấm thảm hình chữ nhật dưới bàn ăn? Đo chiều dài và chiều rộng của khu vực muốn trải thảm, tính diện tích để chọn kích thước thảm phù hợp hoặc tính xem tấm thảm đó có vừa không.
  • Lát gạch backsplash (phần tường giữa mặt bếp và tủ bếp trên)? Đo chiều dài và chiều cao của khu vực đó (thường là hình chữ nhật), tính diện tích để ước lượng số lượng gạch cần mua.
  • Sắp xếp đồ đạc trong ngăn kéo hình chữ nhật? Ước lượng diện tích ngăn kéo và diện tích đáy của các vật dụng để xem chúng có vừa hết không.

• Trong Phòng Khách/Phòng Ngủ:

  • Mua rèm cửa sổ? Chiều rộng của cửa sổ (thường là hình chữ nhật) sẽ quyết định chiều rộng của rèm bạn cần.
  • Sơn tường? Tính diện tích các bức tường hình chữ nhật (lấy chiều dài tường nhân chiều cao phòng, trừ đi diện tích cửa sổ, cửa ra vào) để tính lượng sơn cần thiết. Đừng quên tính cả trần nhà nếu muốn sơn!
  • Mua thảm trải sàn? Đo diện tích khu vực bạn muốn đặt thảm để chọn tấm thảm có kích thước phù hợp.

• Trong Sân Vườn:

  • Làm hàng rào quanh mảnh vườn hình chữ nhật? Đo chiều dài và chiều rộng, tính chu vi để biết tổng chiều dài hàng rào cần mua.
  • Trồng cỏ cho một bãi đất hình chữ nhật? Đo kích thước, tính diện tích để mua đúng lượng hạt giống cỏ hoặc cuộn cỏ.
  • Xây bồn hoa hình chữ nhật? Tính chu vi để biết lượng gạch hoặc vật liệu viền cần dùng, tính diện tích đáy để ước lượng lượng đất cần đổ vào.

• Trong Các Hoạt Động Khác:

  • Mua đất? Diện tích đất đai thường được tính bằng mét vuông (m²) hoặc các đơn vị lớn hơn như sào, mẫu, héc-ta (có thể quy đổi từ m²). Việc hiểu về diện tích giúp bạn định giá hoặc đánh giá miếng đất đó.
  • Đóng khung ảnh? Kích thước ảnh (thường hình chữ nhật) sẽ là chiều dài và chiều rộng để bạn chọn khung có kích thước tương ứng (chu vi khung thường lớn hơn chu vi ảnh một chút).
  • Làm các dự án thủ công, may vá? Cắt vải hoặc giấy theo kích thước hình chữ nhật, tính diện tích hoặc chu vi để đảm bảo đủ vật liệu.

Minh họa ứng dụng công thức tính chu vi và diện tích hình chữ nhật trong các hoạt động đời sống hàng ngày như lát sàn hoặc làm vườn

Qua những ví dụ này, bạn thấy đấy, công thức tính hình chữ nhật không chỉ giới hạn trong sách vở mà thực sự là một kỹ năng sống hữu ích. Nó giúp bạn lập kế hoạch tốt hơn, dự trù kinh phí chính xác hơn và tránh những sai lầm không đáng có trong các công việc liên quan đến không gian và vật liệu.

Để hiểu rõ hơn về các ứng dụng trong cuộc sống và củng cố kiến thức toán học của mình, đôi khi việc xem xét các dạng bài tập từ các cấp độ khác nhau, chẳng hạn như đề thi toán lớp 3 hay lớp 4, có thể mang lại những góc nhìn thú vị và giúp bạn ôn lại kiến thức cơ bản một cách hiệu quả.

Kinh Nghiệm Thực Tế Khi Áp Dụng Công Thức: Chia Sẻ Từ Chuyên Gia (Giả Định)

Việc học công thức là một chuyện, áp dụng vào thực tế lại là chuyện khác. Đôi khi, “lý thuyết là màu xám, còn đời là cây xanh” (một cách nói vui để chỉ sự khác biệt giữa lý thuyết và thực tế). Để có cái nhìn thực tế hơn, chúng ta cùng lắng nghe chia sẻ từ Chú Nam, một kỹ sư xây dựng đã có hơn 20 năm kinh nghiệm trong nghề. Chú Nam đã làm việc với biết bao công trình, từ nhà ở dân dụng đến các tòa nhà lớn, và công thức tính hình chữ nhật luôn là “kim chỉ nam” không thể thiếu trong công việc của chú.

Chú Nam chia sẻ: “Trong nghề xây dựng của chú, việc tính toán diện tích và chu vi hình chữ nhật là ‘chuyện cơm bữa’. Từ việc bóc tách khối lượng vật tư như gạch lát nền, sơn tường, đến tính diện tích sàn, diện tích mái, hay đo đạc ranh giới khu đất, đâu đâu cũng cần dùng đến các công thức cơ bản này. Cái chú thấy quan trọng nhất khi áp dụng vào thực tế không chỉ là nhớ công thức cho đúng, mà là cái bước đầu tiên: đo đạc. Đo phải thật chuẩn, phải cẩn thận từng centimet, nhất là với những công trình lớn, sai một ly là đi một dặm. Nếu đo sai chiều dài hoặc chiều rộng, thì mọi phép tính sau đó đều vô nghĩa, dẫn đến thiếu vật tư hoặc thừa mứa, vừa tốn kém vừa mất thời gian xử lý. Chú thường khuyên anh em thợ là ‘đo đạc kỹ như đo kim cương vậy’, phải kiểm tra đi kiểm tra lại nhiều lần cho chắc ăn. Thứ hai là đơn vị. Làm việc với đủ loại bản vẽ, có cái dùng mét, có cái dùng milimét, phải tỉnh táo để quy đổi về cùng một đơn vị trước khi nhân chia cộng trừ. Chỉ cần nhầm lẫn đơn vị thôi là kết quả sai lệch hàng trăm, hàng nghìn lần, hậu quả khôn lường.”

Chú Nam còn nhấn mạnh thêm: “Một điều nữa mà nhiều bạn trẻ mới vào nghề hay quên là tính đến hao hụt vật tư. Ví dụ lát gạch sàn, diện tích phòng tính ra là 20m² không có nghĩa là chỉ cần mua đúng 20m² gạch. Phải tính thêm phần gạch cắt bỏ ở các góc cạnh, gạch vỡ trong quá trình vận chuyển hoặc thi công, thường phải cộng thêm khoảng 5-10% diện tích tính toán được. Cái này không có trong công thức toán học, nhưng lại là kinh nghiệm xương máu khi áp dụng vào thực tế. Tóm lại, công thức tính hình chữ nhật là nền tảng, nhưng để làm tốt thì cần cả sự cẩn thận, kinh nghiệm thực tế và cái nhìn tổng thể về công việc.”

Những chia sẻ của Chú Nam cho thấy rõ ràng rằng, dù công thức có đơn giản đến đâu, việc áp dụng nó trong môi trường thực tế luôn đòi hỏi sự tỉ mỉ, kinh nghiệm và khả năng xử lý các yếu tố phát sinh ngoài công thức. Đó là sự khác biệt giữa lý thuyết suông và kỹ năng ứng dụng thực tiễn.

Kết Nối Với Các Kiến Thức Khác: Hình Chữ Nhật Trong Chương Trình Học

Khái niệm hình chữ nhật và các công thức tính hình chữ nhật được đưa vào chương trình giáo dục từ khá sớm và được nhắc lại, mở rộng qua nhiều cấp học. Điều này cho thấy tầm quan trọng của nó như một viên gạch nền móng trong hệ thống kiến thức toán học.

Ở bậc tiểu học, cụ thể là từ lớp 3, lớp 4, học sinh bắt đầu làm quen với các hình học cơ bản, trong đó có hình chữ nhật. Các em được học định nghĩa hình chữ nhật, các tính chất đơn giản và trực quan như có 4 góc vuông, các cạnh đối diện bằng nhau. Việc tính chu vi và diện tích hình chữ nhật cũng được giới thiệu một cách dễ hiểu nhất, thường thông qua việc đếm ô vuông đơn vị (cho diện tích) hoặc tính tổng độ dài các cạnh (cho chu vi). Các bài tập chủ yếu xoay quanh việc áp dụng trực tiếp công thức với các số nguyên đơn giản.

Lên lớp 4, lớp 5, độ phức tạp của bài toán tăng lên. Học sinh bắt đầu giải các bài toán có lời văn, các bài toán tìm chiều dài/chiều rộng khi biết diện tích hoặc chu vi và một kích thước còn lại. Các bài toán có thể liên quan đến việc chuyển đổi đơn vị đo đơn giản (ví dụ: từ cm sang dm hoặc m).

Ở bậc trung học cơ sở, hình chữ nhật tiếp tục xuất hiện trong các chủ đề về diện tích và thể tích của các hình khối liên quan như hình hộp chữ nhật. Khái niệm về hệ tọa độ cũng giúp chúng ta mô tả hình chữ nhật bằng các điểm trên mặt phẳng tọa độ, mở ra những cách tiếp cận khác.

Kiến thức về hình chữ nhật và công thức tính toán của nó còn liên quan đến các chủ đề khác trong toán học như tỉ lệ, phân số (trong các bài toán chia diện tích), và thậm chí là đại số (khi giải các bài toán bằng cách lập phương trình).

Việc học toán, đặc biệt là hình học, không chỉ là ghi nhớ công thức mà còn là phát triển tư duy logic, khả năng phân tích vấn đề và giải quyết chúng một cách có hệ thống. Nắm vững các khái niệm cơ bản như công thức tính hình chữ nhật là bước đệm vững chắc để bạn tiếp thu những kiến thức toán học phức tạp hơn sau này.

Phát Triển Tư Duy Và Kỹ Năng Từ Việc Nắm Vững Công Thức Toán Học

Có thể bạn sẽ nghĩ rằng việc học công thức tính hình chữ nhật hay các công thức toán học khác chỉ phục vụ cho việc giải bài tập trên lớp. Tuy nhiên, quá trình học và áp dụng các công thức này thực sự góp phần quan trọng vào việc phát triển nhiều kỹ năng mềm cần thiết cho cuộc sống và công việc.

Khi bạn tiếp cận một bài toán về hình chữ nhật, bạn cần đọc hiểu đề bài, phân tích các thông tin đã cho (chiều dài, chiều rộng, chu vi, diện tích), xác định yêu cầu của bài toán (cần tính gì?). Quá trình này rèn luyện kỹ năng đọc hiểu, phân tích và nhận diện vấn đề.

Tiếp theo, bạn phải chọn công thức phù hợp để giải quyết vấn đề đó. Điều này đòi hỏi khả năng ghi nhớ, hiểu bản chất của công thức và đưa ra lựa chọn đúng đắn từ “kho công cụ” kiến thức của mình.

Sau khi chọn được công thức, bạn thực hiện các phép tính. Đây là lúc sự cẩn thận và chính xác lên ngôi. Một lỗi nhỏ trong cộng, trừ, nhân, chia hoặc sai sót khi chuyển đổi đơn vị có thể làm hỏng toàn bộ kết quả. Kỹ năng tính toán chính xác và tỉ mỉ là vô cùng quan trọng, không chỉ trong toán học mà còn trong quản lý tài chính cá nhân, công việc kế toán, hay bất kỳ công việc nào đòi hỏi sự chính xác về số liệu.

Cuối cùng, sau khi có kết quả, việc kiểm tra lại (như Chú Nam đã nhấn mạnh) giúp bạn phát hiện sai sót và đảm bảo tính đúng đắn. Kỹ năng tự kiểm tra, rà soát lại quy trình làm việc là một thói quen tốt cần được rèn luyện.

Ngoài ra, việc giải các bài toán có lời văn còn giúp bạn phát triển khả năng mô hình hóa vấn đề thực tế thành ngôn ngữ toán học và ngược lại. Bạn học cách biến một tình huống cụ thể trong đời sống (ví dụ: lát sàn nhà) thành một bài toán với các số liệu và công thức, sau đó giải bài toán đó và diễn giải kết quả trở lại ý nghĩa trong đời sống.

Tất cả những kỹ năng này – phân tích, lựa chọn, tính toán chính xác, tự kiểm tra, và mô hình hóa vấn đề – đều là những kỹ năng cốt lõi giúp bạn thành công trong nhiều lĩnh vực. Việc nắm vững công thức tính hình chữ nhật chỉ là một ví dụ nhỏ về cách học toán có thể trang bị cho bạn những công cụ tư duy mạnh mẽ.

Và cũng giống như việc nắm vững các công thức toán học giúp bạn tự tin giải quyết các bài toán về số liệu và không gian, việc trang bị cho mình các kỹ năng giao tiếp, ứng xử, hay khả năng giới thiệu bản thân tiếng anh (một kỹ năng ngày càng cần thiết trong môi trường toàn cầu hóa) cũng giúp bạn “đo lường” và “tính toán” tốt hơn trong các mối quan hệ xã hội và cơ hội nghề nghiệp. Mọi kiến thức và kỹ năng đều bổ trợ cho nhau, giúp chúng ta trở thành những cá nhân toàn diện và sẵn sàng đối mặt với mọi thử thách.

Tổng Kết Về Công Thức Tính Hình Chữ Nhật

Như bạn đã thấy, công thức tính hình chữ nhật không chỉ là một phần kiến thức toán học đơn thuần mà còn là một công cụ vô cùng hữu ích và thiết thực trong cuộc sống. Chúng ta đã cùng nhau tìm hiểu về định nghĩa hình chữ nhật, lý do tại sao việc nắm vững các công thức lại quan trọng, và đi sâu vào hai công thức “vàng” là công thức tính chu vi P = (d + r) * 2 và công thức tính diện tích A = d * r.

Chúng ta cũng đã khám phá cách áp dụng các công thức này qua nhiều ví dụ minh họa chi tiết, từ những bài toán cơ bản nhất đến các dạng bài tập nâng cao hơn như tìm kích thước khi biết chu vi hoặc diện tích. Những lưu ý quan trọng về đơn vị đo, hình vuông, đo đạc thực tế và kiểm tra kết quả đã được chỉ ra để giúp bạn tránh những sai sót không đáng có.

Quan trọng nhất, chúng ta đã thấy được sự hiện diện rộng rãi của công thức tính hình chữ nhật trong đời sống hàng ngày, từ những công việc đơn giản trong nhà bếp hay sân vườn đến các ứng dụng phức tạp hơn trong xây dựng hay thiết kế. Kinh nghiệm từ những người đi trước như Chú Nam càng củng cố thêm rằng, lý thuyết cần đi đôi với thực hành và sự cẩn trọng.

Việc học và làm chủ các công thức toán học như công thức tính hình chữ nhật không chỉ mang lại kiến thức mà còn rèn luyện cho bạn những kỹ năng tư duy quý giá, giúp bạn tự tin hơn khi đối mặt với các vấn đề cần tính toán và phân tích trong cuộc sống.

Hy vọng rằng, bài viết này đã cung cấp cho bạn một cái nhìn toàn diện và sâu sắc về công thức tính hình chữ nhật và tầm quan trọng của nó. Đừng ngần ngại áp dụng những kiến thức này vào thực tế, thử sức với các bài tập khác nhau và bạn sẽ thấy toán học thật gần gũi và hữu ích biết bao! Hãy thực hành thật nhiều và chia sẻ những trải nghiệm, những ứng dụng thú vị của bạn về các công thức này nhé!