Bạn đang “đau đầu” với môn Toán, đặc biệt là phần phương trình tiếp tuyến? Đừng lo lắng! Hầu hết chúng ta đều từng gặp khó khăn khi lần đầu tiếp cận khái niệm này. Từ cấp 1 với phép cộng trừ đơn giản, lên cấp 2 với những bài toán hình học “xoắn não”, rồi bước vào cấp 3 với hàm số, đạo hàm, và đỉnh điểm là Công Thức Phương Trình Tiếp Tuyến. Nghe có vẻ khô khan và phức tạp, nhưng thực ra nó lại là một trong những ứng dụng “đời thường” và thú vị nhất của đạo hàm đấy. Nắm vững công thức này giống như bạn vừa có trong tay một chiếc chìa khóa “vạn năng” để mở ra cánh cửa hiểu sâu hơn về mối liên hệ giữa đại số và hình học, và quan trọng hơn là giải quyết gọn gàng các bài toán liên quan. Bài viết này sẽ cùng bạn “giải mã” từ A đến Z về phương trình tiếp tuyến, biến khái niệm trừu tượng thành thứ gì đó gần gũi, dễ hiểu và áp dụng được ngay.
Phương trình tiếp tuyến là gì?
Bạn cứ hình dung đơn giản thế này: đồ thị hàm số của bạn giống như một con đường cong uốn lượn trên mặt phẳng. Một đường thẳng tiếp tuyến với đồ thị tại một điểm nào đó chính là một con đường thẳng “chạm nhẹ” vào con đường cong tại đúng điểm đó, và tại điểm chạm ấy, hướng đi của đường thẳng trùng hoàn toàn với hướng đi của đường cong.
Nói một cách chính xác hơn về mặt toán học, phương trình tiếp tuyến là phương trình của một đường thẳng có đặc điểm đặc biệt: nó chỉ giao với đồ thị hàm số tại một điểm duy nhất (điểm tiếp xúc) trong một khoảng rất nhỏ xung quanh điểm đó, và “độ dốc” của đường thẳng tại điểm này chính bằng “độ dốc” của đồ thị hàm số tại điểm đó.
Vì sao cần nắm vững công thức phương trình tiếp tuyến?
Công thức phương trình tiếp tuyến không chỉ là một công cụ để “qua môn” hay giải bài tập trên lớp, mà nó còn là nền tảng cực kỳ quan trọng cho nhiều lĩnh vực sau này.
Nắm vững công thức này giúp bạn:
- Hiểu sâu sắc hơn về đạo hàm: Phương trình tiếp tuyến chính là ý nghĩa hình học rõ ràng nhất của đạo hàm. Đạo hàm tại một điểm cho bạn biết “độ dốc” tức thời của đồ thị tại điểm đó, và độ dốc này chính là hệ số góc của đường tiếp tuyến.
- Giải quyết các bài toán liên quan đến tiếp tuyến: Dĩ nhiên rồi! Từ tìm phương trình tiếp tuyến tại một điểm, qua một điểm, song song hay vuông góc với đường khác… tất cả đều cần công thức này.
- Ứng dụng trong các ngành khoa học khác: Tiếp tuyến xuất hiện trong vật lý (vận tốc tức thời, gia tốc), kỹ thuật (thiết kế đường cong, tối ưu hóa), kinh tế (chi phí cận biên, doanh thu cận biên) và nhiều lĩnh vực khác nơi bạn cần phân tích sự thay đổi tức thời.
- Phát triển tư duy phân tích và giải quyết vấn đề: Việc học cách áp dụng công thức vào các bài toán khác nhau rèn luyện khả năng phân tích đề bài, lập kế hoạch giải và thực hiện một cách logic.
Nó giống như việc học công thức tính độ dài đoạn thẳng ở cấp dưới vậy, những kiến thức cơ bản này là viên gạch xây nên những kiến thức phức tạp hơn sau này.
Cốt lõi của công thức phương trình tiếp tuyến nằm ở đâu?
Bản chất của một đường thẳng được xác định bởi hai yếu tố: một điểm mà nó đi qua và độ dốc (hệ số góc) của nó. Với đường tiếp tuyến, hai yếu tố này lại có mối liên hệ đặc biệt với đồ thị hàm số.
Cốt lõi của công thức phương trình tiếp tuyến chính là dựa trên phương trình đường thẳng đi qua một điểm M(x₀, y₀) với hệ số góc k, có dạng:
y – y₀ = k(x – x₀)
Vậy, làm thế nào để tìm được y₀, x₀ và k trong trường hợp của đường tiếp tuyến?
- (x₀, y₀): Đây chính là điểm tiếp xúc giữa đường thẳng và đồ thị hàm số y = f(x). Tọa độ x₀ thường được cho trước hoặc cần tìm. Tọa độ y₀ chính là giá trị của hàm số tại x₀, tức là y₀ = f(x₀).
- k: Đây chính là hệ số góc của đường tiếp tuyến. Và đây là lúc đạo hàm “tỏa sáng”! Hệ số góc của đường tiếp tuyến tại điểm có hoành độ x₀ chính là giá trị của đạo hàm của hàm số tại điểm đó, tức là k = f'(x₀).
Từ đó, chúng ta có công thức phương trình tiếp tuyến cơ bản tại điểm có hoành độ x₀ thuộc đồ thị hàm số y = f(x) là:
y – f(x₀) = f'(x₀)(x – x₀)
Đây chính là công thức “linh hồn” mà bạn cần ghi nhớ thật kỹ.
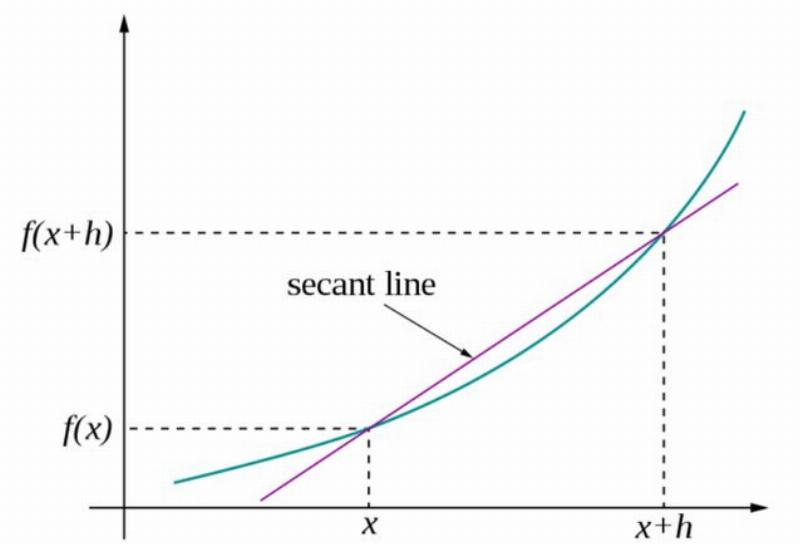 Đồ thị hàm số minh họa phương trình tiếp tuyến tại một điểm tiếp xúc x0 y0 và hệ số góc đạo hàm
Đồ thị hàm số minh họa phương trình tiếp tuyến tại một điểm tiếp xúc x0 y0 và hệ số góc đạo hàm
Làm thế nào để tìm công thức phương trình tiếp tuyến tại một điểm?
Đây là dạng bài tập cơ bản nhất và thường gặp nhất. Khi bạn được cho hàm số y = f(x) và hoành độ điểm tiếp xúc x₀, các bước tìm phương trình tiếp tuyến rất rõ ràng:
- Bước 1: Tính y₀. Thay x₀ vào hàm số y = f(x) để tìm tung độ y₀ của điểm tiếp xúc. Ta có điểm tiếp xúc (x₀, y₀) = (x₀, f(x₀)).
- Bước 2: Tính đạo hàm f'(x). Tìm đạo hàm của hàm số y = f(x). Cần nắm vững các quy tắc tính đạo hàm cơ bản nhé!
- Bước 3: Tính hệ số góc k. Thay x₀ vào đạo hàm vừa tìm được để tính giá trị của đạo hàm tại điểm đó. Đây chính là hệ số góc k = f'(x₀) của đường tiếp tuyến.
- Bước 4: Lập phương trình tiếp tuyến. Thay x₀, y₀ (vừa tính ở Bước 1) và k (vừa tính ở Bước 3) vào công thức chung: y – y₀ = k(x – x₀).
- Bước 5: Rút gọn phương trình. Biến đổi phương trình về dạng y = ax + b hoặc Ax + By + C = 0 cho gọn gàng.
Ví dụ minh họa:
Tìm phương trình tiếp tuyến của đồ thị hàm số y = x² + 2x – 1 tại điểm có hoành độ x₀ = 1.
- Tính y₀: Tại x₀ = 1, y₀ = f(1) = 1² + 2(1) – 1 = 1 + 2 – 1 = 2. Điểm tiếp xúc là (1, 2).
- Tính đạo hàm f'(x): f'(x) = d/dx (x² + 2x – 1) = 2x + 2.
- Tính hệ số góc k: Tại x₀ = 1, k = f'(1) = 2(1) + 2 = 4.
- Lập phương trình: y – y₀ = k(x – x₀) => y – 2 = 4(x – 1).
- Rút gọn: y – 2 = 4x – 4 => y = 4x – 2.
Vậy, phương trình tiếp tuyến tại điểm có hoành độ x = 1 là y = 4x – 2.
Còn các trường hợp khác của phương trình tiếp tuyến thì sao?
Ngoài dạng cơ bản là “tiếp tuyến tại một điểm”, bạn còn có thể gặp các dạng bài yêu cầu tìm phương trình tiếp tuyến khi biết những thông tin khác. Dù đề bài có “biến hóa” thế nào, cốt lõi vẫn là đi tìm được điểm tiếp xúc (x₀, y₀) và hệ số góc k = f'(x₀).
Phương trình tiếp tuyến đi qua một điểm A(x_A, y_A) không thuộc đồ thị
Dạng này “khoai” hơn một chút vì điểm A không phải là điểm tiếp xúc. Ta cần gọi điểm tiếp xúc là M(x₀, y₀). Phương trình tiếp tuyến tại M có dạng: y – y₀ = f'(x₀)(x – x₀).
Vì đường thẳng này đi qua điểm A(x_A, y_A), nên tọa độ của A phải thỏa mãn phương trình này. Thay (x_A, y_A) vào, ta được:
y_A – y₀ = f'(x₀)(x_A – x₀)
Trong đó, y₀ = f(x₀). Thay vào ta có phương trình chứa ẩn duy nhất là x₀:
y_A – f(x₀) = f'(x₀)(x_A – x₀)
Đây là một phương trình (thường là phương trình đại số) theo biến x₀. Nhiệm vụ của bạn là giải phương trình này để tìm các giá trị có thể của x₀. Mỗi giá trị x₀ tìm được sẽ cho một điểm tiếp xúc (x₀, f(x₀)) và một hệ số góc f'(x₀), từ đó bạn viết được phương trình tiếp tuyến tương ứng. Dạng này đòi hỏi kỹ năng giải phương trình tốt.
Phương trình tiếp tuyến song song hoặc vuông góc với đường thẳng cho trước
Dạng này liên quan đến mối quan hệ giữa hệ số góc của hai đường thẳng.
Giả sử đường thẳng cho trước có phương trình y = ax + b (hệ số góc là a).
- Tiếp tuyến song song với đường y = ax + b: Hai đường thẳng song song có cùng hệ số góc. Do đó, hệ số góc của đường tiếp tuyến bằng a. Ta có: k = f'(x₀) = a. Đây là một phương trình theo x₀. Bạn giải phương trình này để tìm x₀, sau đó làm các bước tương tự dạng 1 (tìm y₀ và viết phương trình).
- Tiếp tuyến vuông góc với đường y = ax + b: Hai đường thẳng vuông góc có tích hệ số góc bằng -1 (trừ trường hợp đường thẳng đứng và đường thẳng ngang). Do đó, hệ số góc của đường tiếp tuyến k = -1/a (nếu a ≠ 0). Ta có: f'(x₀) = -1/a. Giải phương trình này tìm x₀ rồi tiếp tục như thường lệ.
Lưu ý: Nếu đường thẳng cho trước là x = c (đường thẳng đứng), thì đường tiếp tuyến vuông góc với nó sẽ là đường thẳng nằm ngang có dạng y = constant (hệ số góc bằng 0). Bạn cần tìm x₀ sao cho f'(x₀) = 0. Ngược lại, nếu đường thẳng cho trước là y = c (đường thẳng ngang, a=0), đường tiếp tuyến vuông góc với nó sẽ là đường thẳng đứng có dạng x = constant. Dạng này cần kiểm tra đạo hàm có “tiệm cận đứng” tại điểm x₀ nào đó không (tức là f'(x₀) không xác định hoặc tiến ra vô cùng).
Những lưu ý “xương máu” khi làm bài tập phương trình tiếp tuyến
Để không bị “vấp ngã” khi giải toán, hãy nhớ những điều sau:
- Kiểm tra kỹ đề bài: Điểm được cho là điểm tiếp xúc (thuộc đồ thị) hay điểm mà tiếp tuyến đi qua (chưa chắc thuộc đồ thị)? Song song hay vuông góc? Với đường thẳng nào? Thông tin này quyết định bạn dùng dạng bài nào.
- Tính đạo hàm chính xác: Đây là bước cực kỳ quan trọng. Sai đạo hàm là sai hết! Ôn lại các công thức và quy tắc tính đạo hàm cơ bản thật kỹ.
- Phân biệt f(x₀) và f'(x₀): f(x₀) là tung độ điểm tiếp xúc, còn f'(x₀) là hệ số góc của tiếp tuyến tại điểm đó. Đừng nhầm lẫn hai giá trị này.
- Giải phương trình cẩn thận: Đặc biệt ở dạng tiếp tuyến đi qua một điểm, phương trình theo x₀ có thể phức tạp (bậc 2, bậc 3…). Hãy giải cẩn thận để không bỏ sót nghiệm nào (vì mỗi nghiệm x₀ là một điểm tiếp xúc và cho một tiếp tuyến).
- Kiểm tra điều kiện: Nếu tiếp tuyến song song hoặc vuông góc, đôi khi có những điều kiện đặc biệt cần kiểm tra (ví dụ, nếu tiếp tuyến song song với đường y=ax+b, nó không thể trùng với đường đó nếu điểm tiếp xúc không nằm trên đường y=ax+b ban đầu).
Tiến sĩ Nguyễn Văn An, giảng viên Toán học chia sẻ: “Nhiều sinh viên thường chỉ nhớ công thức mà quên mất ý nghĩa hình học của nó. Hiểu rằng đạo hàm chính là hệ số góc của tiếp tuyến giúp các em hình dung bài toán rõ ràng hơn và tránh được những sai lầm cơ bản khi xử lý các dạng bài phức tạp hơn.”
Phương trình tiếp tuyến có ứng dụng gì trong đời sống?
Toán học không chỉ nằm trên giấy vở, mà còn len lỏi vào cuộc sống quanh ta. Công thức phương trình tiếp tuyến, dù nghe có vẻ hàn lâm, lại có những ứng dụng rất thực tế:
- Trong vật lý: Khi bạn ném một vật theo quỹ đạo parabol, vận tốc tức thời tại bất kỳ điểm nào trên quỹ đạo lại nằm trên đường tiếp tuyến với quỹ đạo tại điểm đó. Công thức này giúp tính toán chính xác hướng bay của vật.
- Trong kỹ thuật: Khi thiết kế đường cong cho cầu, đường ray tàu lượn siêu tốc hay đường cao tốc, các kỹ sư cần đảm bảo sự chuyển tiếp mượt mà giữa các đoạn cong và thẳng. Điều này liên quan chặt chẽ đến việc đảm bảo các đoạn đường nối có tiếp tuyến chung tại điểm giao nhau, tránh giật cục, nguy hiểm.
- Trong kinh tế: Khái niệm chi phí cận biên hay doanh thu cận biên chính là đạo hàm của hàm tổng chi phí/doanh thu. Đường tiếp tuyến tại một điểm trên đồ thị chi phí/doanh thu cho ta biết sự thay đổi xấp xỉ của chi phí/doanh thu khi sản xuất thêm một đơn vị sản phẩm. Điều này giúp doanh nghiệp đưa ra quyết định tối ưu hóa sản xuất.
- Trong đồ họa máy tính: Các thuật toán vẽ đường cong mượt mà (như đường Bezier) cũng sử dụng khái niệm tiếp tuyến để kiểm soát hình dạng của đường cong.
Hiểu được những ứng dụng này không chỉ giúp bạn thấy Toán học gần gũi hơn, mà còn là động lực để bạn tìm hiểu sâu hơn về toán 10 kết nối tri thức và các cấp độ cao hơn, mở ra cánh cửa đến với nhiều ngành nghề thú vị.
[image-3|ung-dung-phuong-trinh-tiep-tuyen-doi-song|Minh họa ứng dụng phương trình tiếp tuyến trong một bối cảnh đời sống thực tế|A conceptual illustration showing an application of tangent lines. Options: A trajectory of a ball (parabola) with a tangent line indicating instantaneous velocity direction; A simplified diagram of a road curve design showing smooth transitions using tangent concepts; A graph representing marginal cost in economics, showing a tangent line at a point on the total cost curve.|Rèn luyện tư duy qua công thức phương trình tiếp tuyến
Việc học và áp dụng công thức phương trình tiếp tuyến không chỉ mang lại kiến thức toán học, mà còn là một bài tập rèn luyện tư duy cực kỳ hiệu quả. Nó dạy cho bạn cách:
- Phân tích vấn đề phức tạp: Một bài toán phương trình tiếp tuyến có thể có nhiều “lớp” thông tin cần bóc tách: hàm số là gì, điểm cho trước có ý nghĩa gì, mối quan hệ với đường thẳng khác ra sao…
- Lập kế hoạch giải: Bạn phải xác định rõ các bước cần làm: tìm x₀, tìm y₀, tính đạo hàm, tính hệ số góc, viết phương trình…
- Vận dụng kiến thức liên môn: Đôi khi bạn cần kết hợp kiến thức về phương trình đường thẳng, giải phương trình đại số, hay thậm chí một chút hình học giải tích.
- Kiểm tra và tự sửa lỗi: Quá trình làm bài giúp bạn nhận ra sai sót trong tính toán hoặc lập luận và biết cách điều chỉnh.
Tư duy logic, khả năng phân tích và giải quyết vấn đề này không chỉ hữu ích trong việc học toán, mà còn có giá trị trong mọi lĩnh vực của cuộc sống. Nó giúp bạn nhìn nhận các vấn đề một cách có hệ thống, từ đó đưa ra quyết định sáng suốt hơn. Ngay cả trong việc hiểu và phân tích các vấn đề xã hội phức tạp, khả năng suy luận logic và nhìn nhận vấn đề từ nhiều góc độ, tương tự như cách ta phân tích các trường hợp khác nhau của tiếp tuyến, cũng là vô cùng cần thiết.
Kết bài
Hy vọng rằng qua bài viết này, công thức phương trình tiếp tuyến không còn là “ác mộng” đối với bạn nữa. Nó là một công cụ mạnh mẽ, đẹp đẽ và có vô vàn ứng dụng. Hãy dành thời gian ôn lại khái niệm đạo hàm, hệ số góc, và đặc biệt là luyện tập thật nhiều các dạng bài tập khác nhau.
Đừng ngần ngại “thử sức” với các bài toán từ cơ bản đến nâng cao, vì mỗi bài tập là một cơ hội để bạn củng cố kiến thức và rèn luyện kỹ năng. Nếu gặp khó khăn, hãy xem lại các bước, kiểm tra lại phép tính, hoặc tìm kiếm thêm ví dụ. Việc nắm vững công thức phương trình tiếp tuyến chắc chắn sẽ mở ra những cánh cửa mới trong hành trình chinh phục môn Toán và các môn khoa học khác của bạn. Chúc bạn học tốt và gặt hái được nhiều thành công!
