Công Thức Diện Tích Hình Chữ Nhật: Chìa Khóa Vạn Năng Mở Cánh Cửa Hình Học Đời Thường

Chào bạn! Có bao giờ bạn đứng trước một căn phòng trống, một mảnh vườn xinh xắn, hay chỉ đơn giản là một tờ giấy vẽ và tự hỏi: “Làm sao mình biết được ‘chỗ’ mà nó chiếm là bao nhiêu nhỉ?”. Nếu có, thì bạn đang chạm đến một khái niệm cực kỳ căn bản nhưng lại vô cùng quyền năng trong toán học và đời sống: diện tích. Và hôm nay, chúng ta sẽ cùng nhau khám phá “ngôi sao” của các loại diện tích cơ bản – chính là Công Thức Diện Tích Hình Chữ Nhật. Đây không chỉ là một công thức khô khan trên sách vở đâu nhé, nó là chìa khóa giúp chúng ta giải quyết biết bao vấn đề thực tế hàng ngày, từ nhỏ bé như chọn thảm lót sàn đến to lớn như quy hoạch một khu đất. Chỉ với một phép tính đơn giản, bạn đã có thể đo lường, so sánh và lên kế hoạch cho không gian xung quanh mình. Hãy cùng “Mama Yosshino” đi sâu tìm hiểu để thấy công thức này hữu ích đến nhường nào nhé!

Hình chữ nhật là một trong những hình quen thuộc nhất mà chúng ta gặp mỗi ngày. Từ chiếc điện thoại bạn đang cầm, màn hình máy tính đang nhìn, quyển sách đang đọc, viên gạch lát nền nhà, hay ngay cả cái giường bạn ngủ… tất cả đều mang dáng dấp của hình chữ nhật. Việc tính toán diện tích của những vật thể này là điều cần thiết trong rất nhiều tình huống. Nắm vững công thức diện tích hình chữ nhật không chỉ giúp bạn vượt qua các bài kiểm tra toán học một cách dễ dàng, mà còn trang bị cho bạn một kỹ năng sống hữu ích. Nó là nền tảng để bạn hiểu và tính toán diện tích của nhiều hình phức tạp hơn sau này. Tương tự như cách tính diện tích hình thang, việc hiểu rõ bản chất và cách áp dụng công thức này sẽ mở ra nhiều cánh cửa kiến thức mới mẻ và thiết thực.

Vậy, rốt cuộc thì công thức diện tích hình chữ nhật “thần thánh” đó là gì? Nó đơn giản đến mức bạn có thể học thuộc lòng chỉ trong vài giây, nhưng sức mạnh ứng dụng thì lại bất ngờ. Hãy cùng đi vào phần cốt lõi ngay bây giờ!

Công Thức Diện Tích Hình Chữ Nhật Căn Bản: “Chiều Dài Nhân Chiều Rộng”

Đây chính là “bí mật” mà hàng triệu người trên thế giới đều biết và sử dụng:

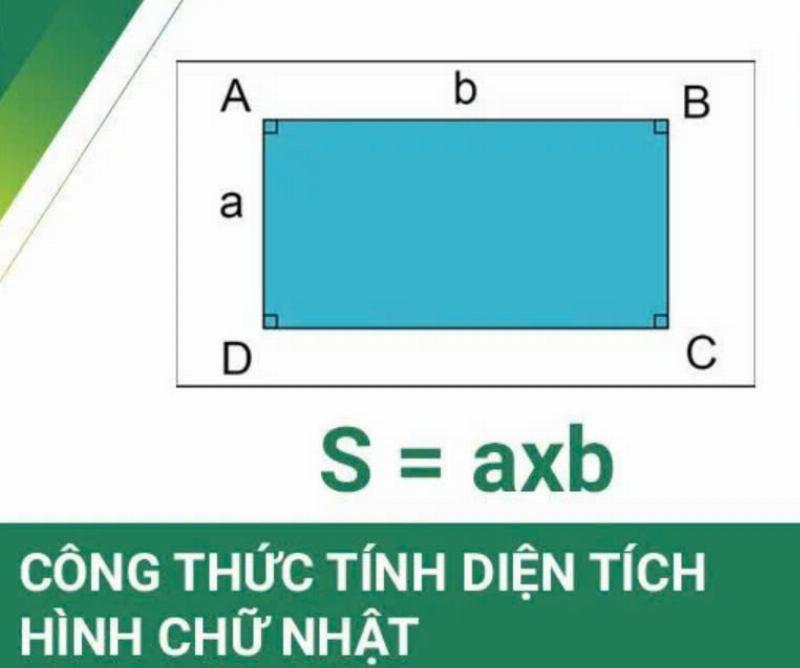
Diện tích Hình chữ nhật = Chiều dài × Chiều rộng

Trong đó:

• Diện tích: Ký hiệu là S hoặc A (Area). Đây là phần không gian bề mặt mà hình chữ nhật đó chiếm giữ. Bạn có thể tưởng tượng diện tích giống như số lượng viên gạch vuông nhỏ bằng nhau cần thiết để lát kín bề mặt hình chữ nhật đó mà không chồng lấn hay để hở.
• Chiều dài: Ký hiệu là a hoặc l (length). Đây là kích thước của cạnh dài hơn của hình chữ nhật. chiều dài hình chữ nhật luôn là một trong hai thông số cần thiết để tính diện tích.
• Chiều rộng: Ký hiệu là b hoặc w (width). Đây là kích thước của cạnh ngắn hơn của hình chữ nhật.

Vậy, công thức được viết gọn lại là:

S = a × b (hoặc S = l × w)

Nghe có vẻ quá đơn giản, đúng không? Nhưng đằng sau sự đơn giản này là cả một nền tảng logic và ứng dụng rộng rãi. Để thực sự “thấm” công thức này, chúng ta cần hiểu rõ từng thành phần của nó.

Hiểu Rõ “Chiều Dài” và “Chiều Rộng” Của Hình Chữ Nhật

Trong hình chữ nhật, có hai cặp cạnh đối diện song song và bằng nhau. Chiều dài và chiều rộng chính là độ dài của hai cạnh kề nhau (gặp nhau tại một đỉnh). Theo quy ước thông thường, cạnh dài hơn được gọi là chiều dài, và cạnh ngắn hơn được gọi là chiều rộng. Tuy nhiên, về mặt toán học, khi áp dụng công thức diện tích hình chữ nhật, bạn nhân hai kích thước của hai cạnh kề nhau, kết quả diện tích vẫn không thay đổi dù bạn gọi cạnh nào là chiều dài hay chiều rộng. Ví dụ, một hình chữ nhật có cạnh 5cm và 3cm. Diện tích sẽ là 5cm × 3cm = 15 cm², hay 3cm × 5cm = 15 cm². Kết quả vẫn là 15 cm².

Điều quan trọng nhất khi xác định chiều dài và chiều rộng để áp dụng công thức diện tích hình chữ nhật là chúng phải là hai cạnh kề nhau và có đơn vị đo giống nhau.

Diện Tích Thực Sự Có Nghĩa Là Gì? Tại Sao Lại Là “Nhân”?

Khái niệm diện tích có thể hơi trừu tượng nếu chỉ nhìn vào công thức. Hãy thử hình dung thế này nhé: Bạn có một hình chữ nhật và muốn “phủ kín” nó bằng những hình vuông nhỏ có cạnh là 1 đơn vị (ví dụ: hình vuông 1cm x 1cm, gọi là 1 cm²).

Giả sử hình chữ nhật của bạn có chiều dài 5 cm và chiều rộng 3 cm.

• Dọc theo chiều dài 5 cm, bạn có thể đặt 5 hình vuông 1cm².
• Dọc theo chiều rộng 3 cm, bạn có thể đặt 3 hình vuông 1cm².

Khi bạn xếp các hàng hình vuông này lại với nhau, bạn sẽ tạo ra một “lưới” hình vuông. Hàng đầu tiên có 5 hình vuông. Hàng thứ hai cũng có 5 hình vuông. Hàng thứ ba cũng có 5 hình vuông. Tổng cộng, bạn có 3 hàng, mỗi hàng 5 hình vuông. Tổng số hình vuông chính là phép nhân: 3 hàng × 5 hình/hàng = 15 hình vuông. Mỗi hình vuông là 1 cm², vậy tổng diện tích là 15 cm².

Đây chính là lý do tại sao công thức diện tích hình chữ nhật lại là phép nhân chiều dài với chiều rộng. Nó mô phỏng quá trình “phủ kín” bề mặt bằng các đơn vị diện tích cơ bản (hình vuông đơn vị).

Hình ảnh minh họa công thức diện tích hình chữ nhật với chiều dài, chiều rộng và vùng diện tích được tô màu

Đơn Vị Đo Diện Tích: Câu Chuyện Của Những Con Số “Vuông”

Khi tính toán diện tích, việc sử dụng đúng đơn vị là cực kỳ quan trọng. Nếu chiều dài và chiều rộng được đo bằng centimet (cm), thì diện tích sẽ có đơn vị là centimet vuông (cm²). Nếu đo bằng mét (m), diện tích là mét vuông (m²). Tương tự, nếu đo bằng kilômét (km), diện tích là kilômét vuông (km²).

Các đơn vị diện tích phổ biến bao gồm:

• Milimét vuông (mm²)
• Centimét vuông (cm²)
• Đềximét vuông (dm²)
• Mét vuông (m²)
• Kilômét vuông (km²)

Ngoài ra, trong đo đạc đất đai, chúng ta còn gặp các đơn vị như:

• Are (a): 1 are = 100 m²
• Hecta (ha): 1 hecta = 100 are = 10,000 m²

Khi áp dụng công thức diện tích hình chữ nhật, bạn phải đảm bảo cả chiều dài và chiều rộng đều ở cùng một đơn vị đo. Nếu chúng ở các đơn vị khác nhau (ví dụ: chiều dài đo bằng mét, chiều rộng đo bằng centimet), bạn cần đổi một trong hai về cùng đơn vị trước khi nhân.

• Ví dụ: Một hình chữ nhật có chiều dài 2m và chiều rộng 50cm. Bạn không thể nhân trực tiếp 2 × 50.
  • Cách 1: Đổi mét sang centimet: 2m = 200cm. Diện tích = 200cm × 50cm = 10,000 cm².
  • Cách 2: Đổi centimet sang mét: 50cm = 0.5m. Diện tích = 2m × 0.5m = 1 m².
  • Lưu ý: 1 m² = 100cm × 100cm = 10,000 cm². Hai kết quả này hoàn toàn khớp nhau.

Việc đổi đơn vị cần sự cẩn thận, đặc biệt là với các đơn vị vuông. Hãy nhớ rằng khi đổi đơn vị dài (mét sang cm là nhân 100), đơn vị diện tích sẽ đổi theo bình phương (m² sang cm² là nhân 100², tức nhân 10,000).

Các Bước Áp Dụng Công Thức Diện Tích Hình Chữ Nhật “Chuẩn Không Cần Chỉnh”

Để tính diện tích hình chữ nhật một cách chính xác, bạn chỉ cần làm theo vài bước đơn giản sau:

1. Xác định hình dạng: Đảm bảo rằng hình bạn cần tính diện tích chính xác là hình chữ nhật. Điều này có nghĩa là nó có bốn cạnh, bốn góc vuông (90 độ), và các cặp cạnh đối diện song song và bằng nhau.
2. Đo kích thước: Đo chiều dài và chiều rộng của hình chữ nhật. Sử dụng thước đo phù hợp (thước kẻ, thước dây) và ghi lại kết quả cẩn thận.
3. Kiểm tra đơn vị: Đây là bước cực kỳ quan trọng! Hãy xem cả hai kích thước (chiều dài và chiều rộng) có cùng đơn vị đo chưa (ví dụ: cả hai đều là cm, hoặc cả hai đều là mét). Nếu chưa, hãy chuyển đổi một trong hai hoặc cả hai về cùng một đơn vị thống nhất. Nên chọn đơn vị phù hợp với mục đích sử dụng (ví dụ: tính diện tích sàn nhà thì dùng m², tính diện tích tờ giấy nhỏ thì dùng cm²).
4. Áp dụng công thức: Lấy giá trị của chiều dài nhân với giá trị của chiều rộng.
   • Diện tích = Chiều dài × Chiều rộng
5. Ghi kết quả kèm đơn vị: Kết quả của phép nhân chính là diện tích. Đừng quên ghi đơn vị diện tích tương ứng (ví dụ: cm², m², ha,…). Đơn vị này phải là đơn vị “vuông” của đơn vị đo độ dài mà bạn đã sử dụng ở bước 3.

Ví dụ minh họa từng bước:

Bạn muốn tính diện tích một chiếc bàn hình chữ nhật.

1. Kiểm tra, chiếc bàn đúng là hình chữ nhật với các góc vuông vắn.
2. Dùng thước dây đo: Chiều dài bàn là 1.5 mét, chiều rộng bàn là 0.8 mét.
3. Kiểm tra đơn vị: Cả hai kích thước đều đang là mét (m). Đơn vị thống nhất rồi, không cần đổi.
4. Áp dụng công thức: Diện tích = Chiều dài × Chiều rộng = 1.5 m × 0.8 m = 1.2.
5. Ghi kết quả: Diện tích chiếc bàn là 1.2 m².

Thật đơn giản phải không? Với những bước này, bạn đã có thể tự tin tính toán diện tích của bất kỳ hình chữ nhật nào trong cuộc sống.

Ứng Dụng Thực Tế Của Công Thức Diện Tích Hình Chữ Nhật Trong Đời Sống

Đừng nghĩ công thức diện tích hình chữ nhật chỉ dành cho học sinh ngồi trong lớp giải toán nhé. Nó có mặt ở khắp mọi nơi quanh ta!

• Thiết kế và Trang trí Nhà cửa:
  • Lát sàn/Ốp tường: Bạn cần biết diện tích sàn nhà hoặc diện tích bức tường để mua đủ gạch, gỗ, thảm lót, hoặc sơn. Nhà sản xuất thường bán theo mét vuông hoặc hộp (ghi rõ phủ được bao nhiêu m²). Tính diện tích phòng giúp bạn tránh mua thừa gây lãng phí hoặc thiếu hụt phải mua bổ sung.
  • May rèm cửa/Ga trải giường: Cần biết diện tích cửa sổ hoặc diện tích mặt giường để tính lượng vải cần dùng.
  • Treo tranh ảnh: Ước lượng diện tích tường trống để bố trí tranh ảnh sao cho cân đối.
• Làm vườn:
  • Tính diện tích mảnh vườn: Để biết cần bao nhiêu hạt giống, cây con, phân bón hoặc lượng đất cần san lấp.
  • Lát lối đi: Tính diện tích lối đi để mua đủ gạch hoặc đá.
• Xây dựng:
  • Tính diện tích móng, sàn, mái nhà: Giúp dự trù vật liệu như bê tông, thép, ngói, tôn.
  • Tính diện tích bề mặt cần trát vữa, sơn bả.
• May mặc và Thủ công:
  • Tính diện tích vải cần cắt: Khi may quần áo, rèm cửa, túi xách…
  • Tính diện tích giấy, bìa: Khi làm thiệp, hộp quà, mô hình…
• Quy hoạch và Địa lý:
  • Tính diện tích thửa đất, cánh đồng.
  • Tính diện tích bản đồ, khu vực.
• Đóng gói:
  • Tính diện tích bề mặt hộp: Để thiết kế nhãn dán, in ấn.

Chỉ với một phép nhân đơn giản, bạn đã có thể đưa ra những quyết định chính xác và tiết kiệm trong rất nhiều công việc. Thật tuyệt vời phải không? Điều này có điểm tương đồng với [essential đi với giới từ gì] trong tiếng Anh, việc hiểu rõ bản chất và cách sử dụng đúng sẽ giúp bạn giao tiếp hiệu quả và chính xác. Trong toán học, việc hiểu rõ bản chất của công thức cũng giúp bạn áp dụng nó một cách hiệu quả nhất.

Hình ảnh minh họa các ứng dụng thực tế của việc tính diện tích hình chữ nhật trong đời sống, ví dụ lát gạch, đo vườn, hoặc tính diện tích sàn nhà.

Các Vấn Đề Thường Gặp Khi Tính Diện Tích Hình Chữ Nhật và Cách Khắc Phục

Dù công thức diện tích hình chữ nhật rất đơn giản, nhưng đôi khi chúng ta vẫn mắc phải một số lỗi nhỏ. Biết trước những lỗi này sẽ giúp bạn tránh được chúng:

• Quên đổi đơn vị: Đây là lỗi phổ biến nhất. Bạn có chiều dài là 2m và chiều rộng là 30cm, nếu nhân trực tiếp 2 × 30 = 60, bạn sẽ được kết quả sai hoàn toàn về đơn vị (nó không phải m² hay cm²). Luôn nhớ kiểm tra và đổi về cùng một đơn vị trước khi tính.
• Nhầm lẫn giữa Diện tích và Chu vi: Diện tích là không gian bên trong, còn chu vi là tổng độ dài các cạnh bao quanh hình đó (tức là a + b + a + b hay 2*(a+b)). Hai khái niệm này hoàn toàn khác nhau và công thức cũng khác nhau. Hãy chắc chắn bạn đang cần tính diện tích (phần “bề mặt”) chứ không phải chu vi (phần “đường viền”).
• Tính toán sai phép nhân: Đôi khi chỉ là một lỗi tính nhẩm hoặc bấm máy tính sai. Hãy kiểm tra lại phép tính của mình.
• Nhầm lẫn giữa các cạnh: Đôi khi trong các bài toán phức tạp, chiều dài và chiều rộng không được cho trực tiếp mà phải suy luận từ các thông tin khác (ví dụ: biết chu vi và một cạnh, hoặc biết đường chéo và một cạnh). Hãy đọc kỹ đề bài và xác định chính xác hai cạnh kề nhau cần dùng cho công thức.
• Sử dụng sai công thức cho hình khác: Công thức Diện tích = Chiều dài × Chiều rộng chỉ áp dụng cho hình chữ nhật và hình vuông (là trường hợp đặc biệt của hình chữ nhật khi chiều dài bằng chiều rộng). Đừng áp dụng bừa bãi cho hình tam giác, hình tròn hay hình bình hành nhé!

Mở Rộng: Hình Vuông – Trường Hợp Đặc Biệt Của Hình Chữ Nhật

Hình vuông là một hình chữ nhật đặc biệt, nơi mà cả bốn cạnh đều bằng nhau. Do đó, chiều dài và chiều rộng của hình vuông là như nhau. Nếu gọi độ dài cạnh của hình vuông là a, thì chiều dài = a và chiều rộng = a.

Áp dụng công thức diện tích hình chữ nhật cho hình vuông, ta có:
Diện tích Hình vuông = Cạnh × Cạnh = a × a = a² (a bình phương)

Vậy, công thức diện tích hình vuông chỉ là một trường hợp riêng của công thức diện tích hình chữ nhật. Hiểu được gốc rễ từ hình chữ nhật sẽ giúp bạn ghi nhớ công thức hình vuông dễ dàng hơn.

Kết Nối Công Thức Diện Tích Hình Chữ Nhật Với Các Hình Khác

Công thức diện tích hình chữ nhật là nền tảng để suy ra hoặc hiểu được công thức diện tích của nhiều hình khác.

• Hình bình hành: Một hình bình hành có thể “biến đổi” thành hình chữ nhật bằng cách cắt một tam giác vuông ở một đầu và ghép sang đầu kia. Do đó, diện tích hình bình hành bằng diện tích hình chữ nhật tương ứng, tức là bằng cạnh đáy nhân với chiều cao (tương tự chiều dài nhân chiều rộng).
• Hình tam giác: Một hình tam giác bất kỳ luôn có diện tích bằng một nửa diện tích của một hình bình hành (hoặc hình chữ nhật) có cùng cạnh đáy và chiều cao. Vì vậy, diện tích tam giác bằng (Đáy × Chiều cao) / 2.

Việc nắm vững công thức diện tích hình chữ nhật giúp bạn dễ dàng tiếp cận và ghi nhớ công thức của các hình khác, thấy được sự liên kết logic trong hình học.

Dạy Công Thức Diện Tích Hình Chữ Nhật Cho Trẻ: Làm Sao Cho Dễ Hiểu?

Giải thích công thức diện tích hình chữ nhật cho trẻ nhỏ có thể rất thú vị nếu bạn dùng các phương pháp trực quan.

• Sử dụng đồ vật thật: Dùng các tấm bìa hình chữ nhật, sách, hộp bút…
• Sử dụng hình vuông đơn vị: Dùng các khối vuông nhỏ (như lego, khối gỗ) hoặc vẽ các ô vuông lên giấy kẻ ô. Cho trẻ xếp các khối vuông này phủ kín bề mặt hình chữ nhật và đếm số lượng.
• Vẽ lưới: Vẽ một hình chữ nhật trên giấy. Chia chiều dài thành các đoạn bằng nhau và chiều rộng thành các đoạn bằng nhau. Kẻ các đường thẳng song song với các cạnh để tạo thành một lưới các hình vuông nhỏ. Cho trẻ đếm số ô vuông. Từ đó, hướng dẫn trẻ nhận ra số ô vuông theo chiều dài và số ô vuông theo chiều rộng, và thấy tổng số ô vuông bằng tích của hai số đó.
• Ví dụ đời thường: “Con xem sàn nhà mình lát bao nhiêu viên gạch vuông?”, “Mẹ cần bao nhiêu mét vuông vải để may cái chăn hình chữ nhật này cho con?”.
• Trò chơi: Tạo các bài tập tính diện tích đơn giản với hình ảnh màu sắc.

Theo Cô Lan Hương, chuyên gia Sư phạm Toán Tiểu học, chia sẻ: “Nắm vững công thức diện tích hình chữ nhật giống như có được chìa khóa đầu tiên để mở cánh cửa vào thế giới hình học. Nó không chỉ giúp giải bài tập, mà còn ứng dụng rất nhiều trong cuộc sống hàng ngày, từ việc lát gạch nền nhà cho đến tính diện tích mảnh vườn nhỏ xinh! Quan trọng là làm sao biến công thức khô khan thành một trò chơi khám phá, một công cụ giải quyết vấn đề thực tế cho các con.”

Điều này nhấn mạnh tầm quan trọng của việc làm cho toán học trở nên gần gũi và có ý nghĩa, tương tự như việc hiểu được [câu chủ đề là gì] khi đọc hoặc viết để nắm bắt ý chính.

Khám Phá Sâu Hơn: Tính Diện Tích Hình Chữ Nhật Khi Chỉ Biết Một Số Thông Tin Khác

Đôi khi, bài toán không cho trực tiếp chiều dài và chiều rộng, mà cho các thông tin khác liên quan đến hình chữ nhật. Lúc này, bạn cần kết hợp công thức diện tích hình chữ nhật với các công thức khác.

• Biết Chu vi và một cạnh:
  • Chu vi hình chữ nhật = 2 × (Chiều dài + Chiều rộng).
  • Nếu biết chu vi và chiều dài, bạn có thể tìm chiều rộng: Chiều rộng = (Chu vi / 2) – Chiều dài.
  • Sau khi tìm được chiều rộng, áp dụng công thức Diện tích = Chiều dài × Chiều rộng.
  • Tương tự nếu biết chu vi và chiều rộng.
• Biết Đường chéo và một cạnh:
  • Trong hình chữ nhật, đường chéo tạo thành một tam giác vuông với hai cạnh kề. Theo định lý Pytago, bình phương đường chéo bằng tổng bình phương hai cạnh góc vuông (chiều dài và chiều rộng).
  • Đường chéo² = Chiều dài² + Chiều rộng²
  • Nếu biết đường chéo (d) và chiều dài (a), bạn có thể tìm chiều rộng (b): b² = d² - a², suy ra b = √(d² - a²).
  • Sau khi tìm được chiều rộng, áp dụng công thức Diện tích = Chiều dài × Chiều rộng.
  • Tương tự nếu biết đường chéo và chiều rộng.

Những bài toán này đòi hỏi bạn phải kết hợp nhiều kiến thức hình học khác nhau, nhưng công thức diện tích hình chữ nhật vẫn là đích đến cuối cùng.

Quan Niệm Về Các Con Số: Từ Đơn Giản Đến Phức Tạp

Việc tính toán diện tích liên quan trực tiếp đến các con số. Từ những con số tự nhiên đơn giản để đếm số viên gạch, đến các số thập phân khi đo đạc chính xác, hay thậm chí là căn bậc hai khi tính toán từ đường chéo. Sự phát triển của các hệ thống số, từ những ký hiệu ban đầu cho đến hệ thập phân mà chúng ta dùng ngày nay, đã tạo điều kiện thuận lợi cho các phép tính như thế này. Dù là tính diện tích hay sắp xếp thứ tự, việc hiểu về con số là nền tảng. Đối với những ai quan tâm đến lịch sử hoặc các hệ thống số khác, việc tìm hiểu về [số la mã từ 1 đến 20] có thể mang lại góc nhìn thú vị về cách con người đã biểu diễn số lượng qua các thời kỳ. Nó cho thấy toán học là một lĩnh vực không ngừng tiến hóa.

Đảm Bảo Tính Chính Xác Khi Áp Dụng Công Thức

Để có kết quả tính diện tích chính xác, bạn cần chú ý vài điểm:

• Đo đạc cẩn thận: Sai số khi đo đạc là nguyên nhân hàng đầu dẫn đến kết quả sai. Hãy đo nhiều lần nếu có thể, đặc biệt với các vật lớn hoặc các cạnh không hoàn hảo.
• Sử dụng dụng cụ đo phù hợp: Thước dây mềm cho các vật thể có bề mặt cong nhẹ, thước thẳng hoặc thước gấp cho các cạnh thẳng và dài, thước kẹp cho các vật nhỏ và cần độ chính xác cao.
• Kiểm tra lại phép tính: Sau khi tính, hãy thử làm lại một lần nữa hoặc nhờ người khác kiểm tra.
• Ước lượng kết quả: Trước khi tính, hãy thử ước lượng xem diện tích khoảng bao nhiêu. Ví dụ, một phòng 4m x 5m thì diện tích khoảng 20m². Nếu bạn tính ra 2m² hoặc 200m², rõ ràng có gì đó sai rồi.

Việc kiểm tra và đối chiếu là một bước không thể thiếu để đảm bảo bạn áp dụng công thức diện tích hình chữ nhật đúng và nhận được kết quả tin cậy.

Hình ảnh một người đang kiểm tra lại phép tính diện tích trên giấy hoặc máy tính, hoặc đang dùng thước đo để xác minh kích thước. Bàn làm việc có thể có sách giáo khoa, máy tính, thước kẻ.

Lời Kết: Nắm Vững Công Thức, Khám Phá Tiềm Năng

Qua bài viết này, chúng ta đã cùng nhau đi từ định nghĩa cơ bản đến những ứng dụng phong phú của công thức diện tích hình chữ nhật. Nó không chỉ là Chiều dài × Chiều rộng trên mặt giấy, mà là một công cụ mạnh mẽ giúp chúng ta tương tác và hiểu hơn về thế giới không gian xung quanh. Từ việc trang trí nhà cửa, làm vườn, xây dựng, cho đến việc giải các bài toán phức tạp hơn, công thức này luôn là nền tảng vững chắc.

Việc nắm vững công thức diện tích hình chữ nhật không chỉ giúp bạn giải quyết các vấn đề thực tế mà còn xây dựng tư duy logic và khả năng suy luận trong toán học. Hãy thực hành thường xuyên, áp dụng công thức vào những tình huống cụ thể trong cuộc sống hàng ngày của bạn. Đừng ngại thử thách bản thân với các bài toán mở rộng.

Hy vọng rằng, sau khi đọc bài viết này, bạn sẽ thấy công thức diện tích hình chữ nhật không còn là một khái niệm xa lạ hay khó nhằn nữa, mà là một người bạn đáng tin cậy, sẵn sàng giúp bạn tính toán và khám phá không gian quanh mình. Hãy bắt đầu áp dụng nó ngay hôm nay và chia sẻ những trải nghiệm thú vị của bạn nhé!