Có lẽ trong ký ức của nhiều người, hình hộp chữ nhật luôn là một “người bạn” quen thuộc từ những ngày đầu tiên chúng ta tiếp xúc với toán học. Từ hộp bánh, thùng sữa, chiếc tủ lạnh cho đến ngôi nhà đang ở, tất cả đều mang dáng dấp của hình hộp chữ nhật. Vậy bạn có bao giờ tự hỏi, làm thế nào để biết được “bề mặt” của những vật thể ấy rộng bao nhiêu? Làm sao để tính toán xem cần bao nhiêu giấy gói để bọc một món quà hình hộp hay bao nhiêu sơn để phủ kín một bức tường? Câu trả lời nằm gọn trong việc nắm vững Công Thức Tính Diện Tích Hình Hộp Chữ Nhật. Đây không chỉ là một kiến thức khô khan trong sách vở mà còn là chìa khóa mở ra vô vàn ứng dụng thực tế, giúp chúng ta “đo lường” thế giới xung quanh một cách chính xác hơn. Bài viết này sẽ cùng bạn đi sâu khám phá mọi ngóc ngách của công thức này, từ lý thuyết đến thực hành, đảm bảo bạn sẽ “thông thạo” nó như thể đang trò chuyện về một người bạn cũ vậy.
Hình hộp chữ nhật là gì và vì sao cần biết công thức tính diện tích của nó?
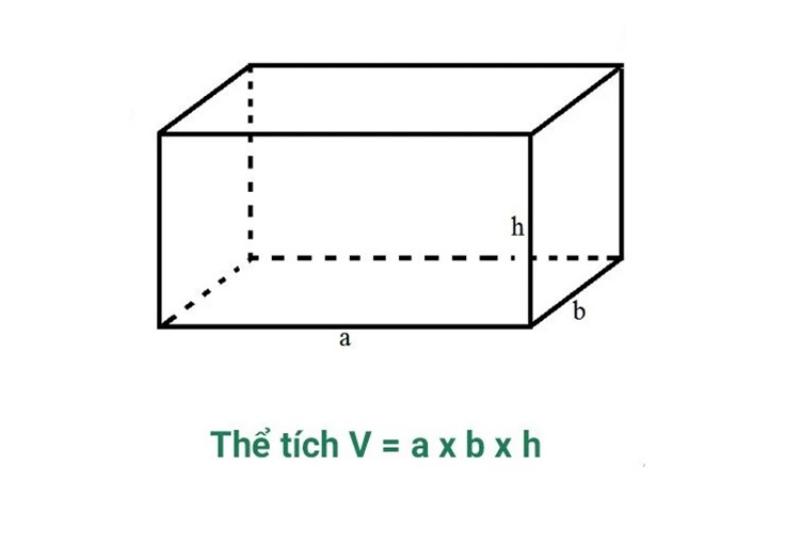
Bạn hình dung mà xem, một chiếc hộp giấy ăn, một viên gạch xây nhà, hay thậm chí là một chiếc điện thoại di động – chúng đều có một điểm chung: đó là hình hộp chữ nhật. Vậy thì, hình hộp chữ nhật là gì? Hiểu đơn giản, nó là một hình không gian ba chiều được tạo thành từ sáu mặt phẳng, mà mỗi mặt đều là một hình chữ nhật. Tưởng tượng một căn phòng của bạn đi, trần nhà, sàn nhà và bốn bức tường chính là sáu mặt của một hình hộp chữ nhật. Nó có ba kích thước cơ bản: chiều dài, chiều rộng và chiều cao, mà các cặp cạnh đối diện thì luôn song song và bằng nhau tăm tắp.
Việc nắm vững công thức tính diện tích hình hộp chữ nhật không chỉ giúp bạn “vượt qua” các bài kiểm tra toán học một cách dễ dàng mà còn là một kỹ năng sống cực kỳ hữu ích. Nó giống như việc bạn có một “siêu năng lực” để tính toán nhanh chóng mọi thứ trong đời thường vậy. Bạn cần mua giấy dán tường cho phòng khách? Cần biết lượng sơn để quét lại ngôi nhà? Hay đơn giản chỉ là muốn gói một món quà thật đẹp mà không bị thiếu giấy? Tất cả đều cần đến công thức này. Khi bạn đã hiểu rõ về khái niệm này, việc áp dụng nó vào các vấn đề thực tế sẽ trở nên cực kỳ linh hoạt và sáng tạo. Thậm chí, việc nắm bắt các công thức cơ bản về hình học còn giúp chúng ta dễ dàng hơn trong việc hình dung và giải quyết các bài toán phức tạp hơn, tương tự như khi ta cần biết diện tích hình vuông công thức để làm nền tảng cho nhiều hình phức tạp khác.
Các loại diện tích của hình hộp chữ nhật: Khác biệt và ý nghĩa
Khi nói đến công thức tính diện tích hình hộp chữ nhật, chúng ta không chỉ nói đến một con số duy nhất. Thực tế, có hai loại diện tích chính mà bạn cần phân biệt rõ ràng: diện tích xung quanh và diện tích toàn phần. Mỗi loại mang một ý nghĩa và ứng dụng riêng biệt, giống như việc bạn cần biết rõ mục đích của mình khi sử dụng một dụng cụ vậy.
Công thức tính diện tích xung quanh hình hộp chữ nhật là gì?
Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích của bốn mặt bên, hay nói cách khác, đó là “bức tường bao quanh” của khối hộp mà không tính đến phần “trần” và “sàn”. Đây là câu trả lời trực tiếp cho việc bạn muốn biết cần bao nhiêu vật liệu để phủ kín các mặt bên của một vật thể hình hộp.
Để tính diện tích xung quanh, bạn cần xác định chu vi đáy của hình hộp chữ nhật rồi nhân với chiều cao. Chu vi đáy được tính bằng cách lấy tổng chiều dài và chiều rộng rồi nhân đôi. Cụ thể, công thức tính diện tích hình hộp chữ nhật xung quanh là:
Diện tích xung quanh (Sxq) = (Chiều dài + Chiều rộng) x 2 x Chiều cao
- Ví dụ minh họa: Giả sử bạn có một chiếc thùng carton dài 50cm, rộng 30cm và cao 40cm.
- Chu vi đáy = (50 + 30) x 2 = 80 x 2 = 160cm
- Diện tích xung quanh = 160cm x 40cm = 6400 cm²
Diện tích xung quanh thường được ứng dụng khi bạn cần tính diện tích các bề mặt không bao gồm mặt đáy và mặt trên. Chẳng hạn, khi bạn muốn sơn lại bốn bức tường của một căn phòng, hoặc dán nhãn bao quanh một chiếc hộp đựng sản phẩm. Việc nắm chắc công thức này giúp bạn ước lượng vật liệu cần thiết một cách chính xác, tránh lãng phí.
Công thức tính diện tích toàn phần hình hộp chữ nhật được xác định như thế nào?
Diện tích toàn phần của hình hộp chữ nhật là tổng diện tích của tất cả sáu mặt của nó: bốn mặt bên (diện tích xung quanh) và hai mặt đáy (mặt trên và mặt dưới). Đây là con số bạn cần khi muốn biết tổng diện tích bề mặt của toàn bộ khối hộp.
Bạn có thể tính diện tích toàn phần bằng hai cách. Cách thứ nhất là lấy diện tích xung quanh cộng với diện tích của hai mặt đáy. Mỗi mặt đáy là một hình chữ nhật có diện tích bằng chiều dài nhân chiều rộng.
Diện tích toàn phần (Stp) = Diện tích xung quanh + 2 x Diện tích đáy
Trong đó: Diện tích đáy = Chiều dài x Chiều rộng
Cách thứ hai, bạn có thể tính tổng diện tích của ba cặp mặt đối diện rồi cộng lại:
Diện tích toàn phần (Stp) = 2 x (Chiều dài x Chiều rộng + Chiều dài x Chiều cao + Chiều rộng x Chiều cao)
- Ví dụ minh họa: Vẫn chiếc thùng carton dài 50cm, rộng 30cm và cao 40cm.
- Diện tích đáy = 50cm x 30cm = 1500 cm²
- Diện tích xung quanh = 6400 cm² (tính ở trên)
- Cách 1: Diện tích toàn phần = 6400 cm² + 2 x 1500 cm² = 6400 cm² + 3000 cm² = 9400 cm²
- Cách 2: Diện tích toàn phần = 2 x (50×30 + 50×40 + 30×40) = 2 x (1500 + 2000 + 1200) = 2 x 4700 = 9400 cm²
 Minh họa các mặt của hình hộp chữ nhật giúp hiểu rõ công thức tính diện tích xung quanh và toàn phần
Minh họa các mặt của hình hộp chữ nhật giúp hiểu rõ công thức tính diện tích xung quanh và toàn phần
Việc phân biệt rõ ràng giữa diện tích xung quanh và diện tích toàn phần là cực kỳ quan trọng. Nó giúp bạn tránh nhầm lẫn và áp dụng đúng công thức tính diện tích hình hộp chữ nhật cho từng trường hợp cụ thể. Giống như việc bạn không thể dùng một chiếc kìm để đóng đinh vậy, mỗi công thức có một mục đích riêng của nó.
“Việc nắm vững cả hai loại diện tích, xung quanh và toàn phần, không chỉ là hiểu công thức. Đó là khả năng hình dung vật thể trong không gian và áp dụng kiến thức để giải quyết vấn đề thực tế. Như xây một ngôi nhà, bạn cần biết diện tích tường để sơn (xung quanh) và diện tích mái, sàn để lợp, lát (toàn phần). Toán học luôn ẩn chứa trong đời sống một cách rất tự nhiên.” – Tiến sĩ Nguyễn Thanh Mai, một chuyên gia hàng đầu về toán học ứng dụng, từng chia sẻ.
Ứng dụng thực tế của công thức tính diện tích hình hộp chữ nhật trong cuộc sống hàng ngày
Bạn có tin rằng, công thức tính diện tích hình hộp chữ nhật không chỉ nằm yên trong sách giáo khoa mà nó còn “nhảy múa” xung quanh chúng ta mỗi ngày? Từ những vật dụng quen thuộc đến các công trình kiến trúc đồ sộ, dấu ấn của công thức này hiện diện khắp nơi.
- Đóng gói và Bao bì: Bạn đã bao giờ mua một hộp bánh, một thùng sữa hay một chiếc điện thoại mới chưa? Nhà sản xuất cần biết chính xác diện tích bề mặt của chiếc hộp để tính toán lượng vật liệu cần dùng, từ đó tối ưu chi phí và thiết kế bao bì sao cho đẹp mắt, vừa vặn. Đây là một ứng dụng rất phổ biến của công thức này.
- Xây dựng và Trang trí nội thất: Khi một kiến trúc sư thiết kế một ngôi nhà, họ cần tính toán diện tích các bức tường, sàn nhà, trần nhà để ước tính lượng sơn, gạch lát, vật liệu ốp trần. Hay đơn giản hơn, khi bạn muốn dán một bức tranh lớn lên tường hoặc treo rèm cửa, việc nắm được diện tích bề mặt sẽ giúp bạn chọn kích thước phù hợp.
- Thiết kế và Nghệ thuật: Các nhà thiết kế đồ họa, nghệ sĩ sắp đặt cũng thường xuyên làm việc với các khối hình học. Họ có thể sử dụng công thức này để tính toán lượng vật liệu cho các tác phẩm điêu khắc, mô hình 3D, hoặc thậm chí là khi tạo ra các hiệu ứng thị giác trên màn hình.
- Nông nghiệp và Vận tải: Trong nông nghiệp, việc tính toán diện tích các bồn chứa nước, thùng ủ phân, hay chuồng trại hình hộp cũng rất quan trọng để đảm bảo dung tích phù hợp và vật liệu bền vững. Trong vận tải, việc xếp hàng hóa vào container, thùng xe tải cũng đòi hỏi người ta phải hiểu rõ về kích thước và diện tích các bề mặt để tối ưu không gian và đảm bảo an toàn.
- Giáo dục và Đồ chơi: Ngay cả trong giáo dục, khi dạy trẻ về hình khối, việc cho trẻ tự tay đo đạc, tính toán diện tích các khối hộp đồ chơi, hộp bút cũng là cách tuyệt vời để biến kiến thức trừu tượng thành trải nghiệm thực tế, giúp các em dễ hình dung và ghi nhớ lâu hơn.
 Minh họa các ứng dụng thực tế của công thức tính diện tích hình hộp chữ nhật trong đời sống
Minh họa các ứng dụng thực tế của công thức tính diện tích hình hộp chữ nhật trong đời sống
Nhờ công thức tính diện tích hình hộp chữ nhật, chúng ta có thể làm được nhiều điều hơn là chỉ giải bài tập. Nó giúp chúng ta tiết kiệm chi phí, tối ưu hóa vật liệu, và đưa ra những quyết định thông minh hơn trong cuộc sống hàng ngày.
Các bước giải bài toán tính diện tích hình hộp chữ nhật một cách dễ hiểu
Giống như việc bạn học cách nấu một món ăn ngon, việc giải một bài toán toán học cũng cần có một quy trình rõ ràng và từng bước cụ thể. Đối với công thức tính diện tích hình hộp chữ nhật, bạn chỉ cần làm theo các bước đơn giản sau đây, đảm bảo bạn sẽ “ghi điểm” tuyệt đối trong mọi tình huống.
- Đọc kỹ đề bài và xác định yêu cầu: Đây là bước quan trọng nhất. Hãy đọc đi đọc lại đề bài ít nhất hai lần để đảm bảo bạn hiểu rõ câu hỏi đang muốn bạn tính diện tích xung quanh hay diện tích toàn phần của hình hộp chữ nhật. Bạn cũng cần gạch chân hoặc ghi chú các thông số đã cho (chiều dài, chiều rộng, chiều cao).
- Xác định các đại lượng đã biết: Ghi ra giấy các số đo cụ thể mà đề bài cung cấp. Ví dụ: Chiều dài (d) = …, Chiều rộng (r) = …, Chiều cao (c) = … Luôn chú ý đến đơn vị đo (cm, m, dm, km…) và đảm bảo chúng thống nhất. Nếu không, bạn cần thực hiện bước quy đổi đơn vị. Việc này cũng tương tự như khi chúng ta tìm cách phân loại các thông tin để có mấy loại môi trường sống của sinh vật vậy, cần phải xác định rõ “đối tượng” và “thuộc tính” của nó trước khi đi sâu vào phân tích.
- Chọn công thức phù hợp: Dựa vào yêu cầu của đề bài (diện tích xung quanh hay diện tích toàn phần), hãy chọn đúng công thức tính diện tích hình hộp chữ nhật mà chúng ta đã tìm hiểu ở phần trên.
- Nếu yêu cầu tính diện tích xung quanh:
Sxung quanh = (dài + rộng) x 2 x cao - Nếu yêu cầu tính diện tích toàn phần:
Stoàn phần = Sxung quanh + 2 x (dài x rộng)hoặcStoàn phần = 2 x (dài x rộng + dài x cao + rộng x cao)
- Nếu yêu cầu tính diện tích xung quanh:
- Thực hiện tính toán: Thay các giá trị đã biết vào công thức và thực hiện các phép tính theo đúng thứ tự ưu tiên (nhân chia trước, cộng trừ sau, trong ngoặc trước). Hãy cẩn thận từng chút một để tránh sai sót.
- Ghi kết quả và đơn vị: Sau khi tính toán xong, đừng quên ghi rõ kết quả cuối cùng kèm theo đơn vị diện tích tương ứng (cm², m², dm²…).
- Bài tập ví dụ chi tiết:
- Đề bài: Một bể cá hình hộp chữ nhật có chiều dài 80 cm, chiều rộng 40 cm và chiều cao 50 cm. Người ta muốn dán giấy màu vào bốn mặt xung quanh của bể. Hỏi cần bao nhiêu cm² giấy màu?
- Phân tích:
- Yêu cầu: Tính diện tích xung quanh.
- Các đại lượng đã biết: Chiều dài = 80 cm, Chiều rộng = 40 cm, Chiều cao = 50 cm.
- Đơn vị: Đã thống nhất (cm).
- Thực hiện:
- Áp dụng công thức tính diện tích hình hộp chữ nhật xung quanh:
Sxung quanh = (80 + 40) x 2 x 50Sxung quanh = 120 x 2 x 50Sxung quanh = 240 x 50Sxung quanh = 12000 cm²
- Áp dụng công thức tính diện tích hình hộp chữ nhật xung quanh:
- Kết quả: Cần 12000 cm² giấy màu để dán bốn mặt xung quanh của bể cá.
Việc giải bài toán không chỉ đơn thuần là tìm ra một con số. Nó còn rèn luyện cho chúng ta tư duy logic, khả năng phân tích và giải quyết vấn đề. Đôi khi, một bài toán tưởng chừng phức tạp lại có thể được giải quyết một cách gọn gàng nếu bạn biết cách cách giải bài toán bằng cách lập phương trình hay các phương pháp tiếp cận khác phù hợp.
Những sai lầm thường gặp khi áp dụng công thức tính diện tích hình hộp chữ nhật và cách khắc phục
Mặc dù công thức tính diện tích hình hộp chữ nhật có vẻ đơn giản, nhưng không ít người vẫn mắc phải những sai lầm cơ bản. Đừng lo lắng, đó là chuyện bình thường khi học hỏi điều mới. Quan trọng là chúng ta nhận ra và biết cách khắc phục.
- Nhầm lẫn giữa diện tích xung quanh và diện tích toàn phần: Đây là lỗi phổ biến nhất. Nhiều người khi đọc đề bài không kỹ, tự động áp dụng công thức diện tích toàn phần khi đề chỉ yêu cầu diện tích xung quanh, hoặc ngược lại.
- Cách khắc phục: Luôn gạch chân hoặc khoanh tròn từ khóa “xung quanh” hay “toàn phần” trong đề bài. Tự hỏi bản thân: “Bài toán này muốn tôi tính phần ‘vỏ’ hay cả phần ‘vỏ’ và ‘đáy’?”
- Sai đơn vị đo hoặc không quy đổi đơn vị: Đề bài có thể cho chiều dài bằng mét, chiều rộng bằng decimet và chiều cao bằng centimet. Nếu bạn cứ thế mà thay số vào, kết quả chắc chắn sẽ sai.
- Cách khắc phục: Trước khi bắt đầu tính toán, hãy kiểm tra kỹ tất cả các đơn vị. Đảm bảo chúng đều là một loại đơn vị duy nhất (ví dụ, tất cả là mét, hoặc tất cả là centimet). Nếu không, hãy thực hiện bước quy đổi đơn vị ngay lập tức. Ví dụ, 1m = 10dm = 100cm.
- Tính toán nhầm lẫn các phép tính: Dù công thức không quá phức tạp, nhưng việc tính nhẩm sai hoặc bấm máy tính nhầm vẫn có thể xảy ra, đặc biệt khi có nhiều số.
- Cách khắc phục: Hãy thực hiện từng bước một. Viết rõ ràng các phép tính trung gian. Sử dụng máy tính cẩn thận và kiểm tra lại kết quả ít nhất hai lần. Đặc biệt, hãy kiểm tra lại bằng cách nhẩm lại các bước hoặc sử dụng công thức biến thể nếu có (như hai cách tính diện tích toàn phần).
- Không hình dung được hình hộp chữ nhật trong không gian: Đôi khi, việc đọc các con số khô khan khiến chúng ta khó hình dung ra vật thể thật, dẫn đến việc nhầm lẫn giữa chiều dài, chiều rộng, chiều cao.
- Cách khắc phục: Hãy lấy một vật thể hình hộp chữ nhật có sẵn trong nhà (ví dụ: hộp bánh, quyển sách, điện thoại) và hình dung nó trong đầu. Dùng ngón tay chỉ vào chiều dài, chiều rộng, chiều cao của vật thể đó khi đọc đề bài. Hoặc bạn có thể vẽ phác thảo nhanh hình hộp chữ nhật và ghi các kích thước lên đó.
Việc nhận diện và tránh những sai lầm này sẽ giúp bạn tự tin hơn rất nhiều khi áp dụng công thức tính diện tích hình hộp chữ nhật vào cả bài tập lẫn đời sống. Sai lầm là một phần của quá trình học hỏi, đừng ngần ngại học từ chúng!
Tối ưu hóa việc học công thức tính diện tích hình hộp chữ nhật cho mọi lứa tuổi
Việc học toán, đặc biệt là hình học, không nhất thiết phải khô khan. Với công thức tính diện tích hình hộp chữ nhật, chúng ta có rất nhiều cách để biến quá trình học thành một trải nghiệm thú vị, hiệu quả cho cả trẻ em và người lớn.
- Học qua trải nghiệm thực tế:
- Cho trẻ em: Hãy biến những vật dụng trong nhà thành “công cụ” học tập. Cùng con đo đạc chiếc hộp bánh, thùng sữa, hay thậm chí là cái tủ lạnh. Sau đó, cùng nhau tính diện tích xung quanh và toàn phần của chúng. Điều này giúp các bé hình dung rõ ràng hơn về khái niệm, không còn thấy nó xa vời nữa.
- Cho người lớn: Khi bạn đi mua sắm đồ đạc, hãy thử ước tính diện tích của một chiếc bàn, một cái kệ sách để xem có vừa không, hay cần bao nhiêu giấy dán để trang trí một góc phòng. Việc áp dụng kiến thức vào những tình huống cụ thể sẽ giúp bạn ghi nhớ công thức lâu hơn và linh hoạt hơn trong việc sử dụng.
- Sử dụng mô hình và đồ vật trực quan:
- Tự làm mô hình: Cắt bìa cứng và dán lại thành một hình hộp chữ nhật không nắp, sau đó dán thêm các “mặt” còn thiếu. Tháo ra và trải phẳng để thấy rõ các mặt và dễ dàng tính toán diện tích từng phần. Đây là cách tuyệt vời để “mổ xẻ” và hiểu sâu về cấu trúc của hình hộp.
- Sử dụng các khối hình học có sẵn: Các bộ đồ chơi xếp hình, các khối gỗ học toán thường có hình hộp chữ nhật. Hãy dùng chúng để thực hành đo đạc và tính toán.
- Học qua các trò chơi và ứng dụng:
- Ngày nay có rất nhiều ứng dụng học toán, trò chơi giáo dục trên điện thoại, máy tính bảng giúp củng cố kiến thức hình học một cách vui vẻ. Hãy tìm kiếm những trò chơi liên quan đến việc đo đạc, tính toán diện tích để luyện tập.
- Bạn có thể tự tạo ra các “thử thách” nhỏ cho bản thân hoặc cho con: “Nếu muốn gói món quà này bằng giấy hoa, con cần bao nhiêu giấy?” hay “Chiếc tủ này có bao nhiêu diện tích bề mặt nếu mẹ muốn dán decal lên toàn bộ?”.
- Liên hệ với các môn học khác và đời sống:
- Kết nối với môn Mỹ thuật: Thiết kế và trang trí hộp quà, làm mô hình kiến trúc nhỏ.
- Kết nối với Vật lý: Tính thể tích, khối lượng của các vật thể hình hộp.
- Khi bạn biết cách viết thiệp 20 11 tặng cô giáo một cách ý nghĩa, bạn có thể áp dụng kiến thức về kích thước và diện tích để chọn chất liệu giấy, trang trí thiệp sao cho cân đối và đẹp mắt nhất. Việc này giúp kiến thức không chỉ nằm trong một lĩnh vực mà có thể lan tỏa, tạo nên sự kết nối và tư duy đa chiều.
Bằng cách biến việc học thành một hành trình khám phá, bạn sẽ thấy công thức tính diện tích hình hộp chữ nhật không còn là “ác mộng” mà trở thành một công cụ hữu ích, giúp bạn hiểu rõ hơn về thế giới xung quanh mình.
Các yếu tố ảnh hưởng đến việc tính toán và sử dụng công thức này hiệu quả
Để việc áp dụng công thức tính diện tích hình hộp chữ nhật đạt hiệu quả cao nhất, chúng ta cần lưu ý một vài yếu tố quan trọng, đôi khi tưởng chừng nhỏ nhặt nhưng lại có thể làm thay đổi hoàn toàn kết quả.
- Độ chính xác của số đo:
- Tầm quan trọng: Đây là yếu tố then chốt. Nếu số đo chiều dài, chiều rộng, chiều cao không chính xác (ví dụ, bạn đo lệch 1-2mm), thì kết quả diện tích cuối cùng cũng sẽ sai lệch. Trong các ngành như xây dựng, thiết kế, một sai số nhỏ cũng có thể dẫn đến hậu quả lớn (vật liệu bị thiếu hoặc thừa, không lắp ráp vừa).
- Cách đảm bảo: Luôn sử dụng dụng cụ đo chính xác (thước dây, thước kẻ, thước kẹp). Đo lặp lại nhiều lần để đảm bảo tính nhất quán của số liệu. Nếu có thể, hãy nhờ người khác kiểm tra lại phép đo của bạn.
- Mục đích sử dụng diện tích:
- Ảnh hưởng: Mục đích cuối cùng của việc tính diện tích sẽ quyết định bạn cần diện tích xung quanh hay toàn phần, và mức độ chính xác cần thiết.
- Ví dụ: Nếu bạn chỉ muốn ước tính lượng giấy gói quà một cách tương đối, sai số vài cm² không thành vấn đề. Nhưng nếu bạn đang thiết kế một bộ phận máy móc cần độ chính xác cao, thì từng milimet vuông cũng quan trọng.
- Cách cân nhắc: Luôn tự hỏi: “Kết quả diện tích này sẽ dùng để làm gì?” Từ đó, bạn sẽ biết cần đầu tư bao nhiêu thời gian và công sức để đạt được độ chính xác mong muốn.
- Công cụ hỗ trợ tính toán:
- Máy tính cầm tay: Đối với các số liệu phức tạp hoặc số thập phân, máy tính là người bạn không thể thiếu. Hãy đảm bảo bạn biết cách sử dụng máy tính một cách thành thạo, đặc biệt là các phím chức năng cơ bản.
- Phần mềm chuyên dụng: Trong lĩnh vực thiết kế, kiến trúc, kỹ thuật, các phần mềm CAD (Computer-Aided Design) như AutoCAD, SketchUp, Revit… có thể tự động tính toán diện tích bề mặt của các vật thể 3D một cách nhanh chóng và chính xác.
- Cách tối ưu: Chọn công cụ phù hợp với độ phức tạp của bài toán và nhu cầu của bạn. Đừng ngại tìm hiểu và tận dụng các công nghệ hiện đại để tăng hiệu quả công việc.
 Hình ảnh các công cụ đo lường và tính toán diện tích hình hộp chữ nhật
Hình ảnh các công cụ đo lường và tính toán diện tích hình hộp chữ nhật
Bằng cách chú ý đến những yếu tố này, bạn không chỉ áp dụng công thức tính diện tích hình hộp chữ nhật một cách máy móc mà còn hiểu được “linh hồn” của nó, từ đó nâng cao kỹ năng giải quyết vấn đề của mình lên một tầm cao mới.
Lời khuyên từ chuyên gia: Nắm vững công thức để mở rộng tư duy hình học
Nắm vững công thức tính diện tích hình hộp chữ nhật không chỉ là mục tiêu cuối cùng, mà nó còn là cánh cửa mở ra những hiểu biết sâu sắc hơn về thế giới hình học xung quanh chúng ta. Đối với những ai đang trên hành trình chinh phục toán học, hay đơn giản là muốn trang bị cho mình những kỹ năng sống thiết yếu, đây là một vài lời khuyên từ những người có kinh nghiệm:
- Học chắc gốc, hiểu sâu bản chất: Đừng chỉ học thuộc lòng công thức. Hãy cố gắng hiểu tại sao công thức lại như vậy. Tại sao diện tích xung quanh lại là chu vi đáy nhân chiều cao? Tại sao diện tích toàn phần lại cộng thêm hai mặt đáy? Khi bạn hiểu được bản chất, bạn sẽ không bao giờ quên và có thể tự suy luận ra công thức nếu chẳng may quên mất. Việc này cũng giống như việc bạn cần hiểu rõ đặc điểm của từng bộ phận của một loại rau như rau cài răng lược là gì để biết cách trồng và chăm sóc nó hiệu quả vậy – mỗi chi tiết nhỏ đều quan trọng.
- Thực hành đều đặn, không ngừng nghỉ: “Học đi đôi với hành.” Không có con đường tắt nào để thành thạo một kiến thức toán học ngoài việc thực hành thường xuyên. Hãy tự đặt ra các bài toán cho mình, hoặc tìm kiếm các bài tập trên mạng, trong sách giáo khoa. Càng làm nhiều, bạn càng tự tin và nhuần nhuyễn.
- Biến toán học thành trò chơi: Hãy tìm cách lồng ghép toán học vào các hoạt động hàng ngày. Cùng con xây dựng một ngôi nhà từ các khối gỗ, tính toán xem cần bao nhiêu giấy để trang trí một chiếc hộp đựng đồ chơi. Khi toán học trở thành một phần của trò chơi, nó sẽ không còn là gánh nặng mà trở thành niềm vui khám phá.
- Kiên nhẫn và không ngại sai lầm: Ai cũng có lúc mắc lỗi, đặc biệt là khi học một kiến thức mới. Quan trọng là bạn học được gì từ những sai lầm đó. Đừng nản lòng nếu lần đầu bạn tính sai. Hãy xem đó là cơ hội để bạn nhìn lại, tìm ra nguyên nhân và khắc phục.
- Luôn kết nối kiến thức với thực tế: Toán học không phải là thứ xa vời mà nó hiện diện khắp mọi nơi. Khi bạn nhìn thấy một chiếc tủ, một cái bàn, hãy thử hình dung và ước tính diện tích của chúng. Việc kết nối lý thuyết với thực tế sẽ giúp bạn thấy toán học thật hữu ích và thú vị.
Việc nắm vững công thức tính diện tích hình hộp chữ nhật là một bước đệm quan trọng giúp bạn mở rộng tư duy về hình học không gian. Từ đó, bạn có thể dễ dàng tiếp thu các khái niệm phức tạp hơn, và ứng dụng toán học vào giải quyết các vấn đề trong cuộc sống một cách chủ động và sáng tạo.
Như vậy, chúng ta đã cùng nhau đi qua một hành trình khám phá đầy đủ và chi tiết về công thức tính diện tích hình hộp chữ nhật. Từ định nghĩa cơ bản, sự khác biệt giữa diện tích xung quanh và toàn phần, cho đến vô vàn ứng dụng thực tế trong đời sống, cách giải bài tập chi tiết và cả những lời khuyên hữu ích để học tập hiệu quả. Hy vọng rằng, qua bài viết này, bạn không chỉ nắm vững kiến thức mà còn tìm thấy niềm vui trong việc ứng dụng toán học vào thế giới xung quanh.
Việc thấu hiểu công thức này không chỉ giúp bạn giải quyết các bài toán trên giấy mà còn trang bị cho bạn một “cầm nang” hữu ích để tính toán, ước lượng trong các tình huống thực tế, từ việc sửa sang nhà cửa cho đến việc gói ghém món quà ý nghĩa. Hãy thử áp dụng ngay hôm nay và chia sẻ trải nghiệm của bạn nhé. Chắc chắn bạn sẽ thấy công thức tính diện tích hình hộp chữ nhật không còn là điều gì đó xa lạ, mà là một công cụ mạnh mẽ trong tay bạn!
